Floyd算法
所有顶点对之间的最短路径问题是:对于给定的有向网络G=(V,E),要对G中任意两个顶点v,w(v不等于w),找出v到w的最短路径。当然我们可以n次执行DIJKSTRA算法,用FLOYD则更为直接,两种方法的时间复杂度都是一样的。
1.定义概览
Floyd-Warshall算法(Floyd-Warshall algorithm)是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N3),空间复杂度为O(N2)。
2.算法描述
1)算法思想原理:
Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在)
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
2).算法描述:
a.从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
b.对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
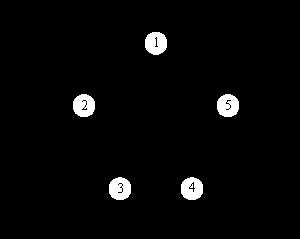
以下面的有向网络为例:


1 #include<stdio.h>
2 #define n 5 //结点数目
3 #define maxsize 160 //表示两点间不可达
4 int path[n][n];//路径矩阵
5 void floyd(int A[][n],int C[][n]); //A是路径长度矩阵,C是有向网络G的带权邻接矩阵
6 void main()
7 {
8 printf(" ——所有顶点对之间的最短路径:Floyd算法——\n");
9 printf("(160为无穷远,不可达)\n");
10 int A[n][n],C[n][n]={
11 {0,10,maxsize,30,100},
12 {maxsize,0,50,maxsize,maxsize},
13 {maxsize,maxsize,0,maxsize,10},
14 {maxsize,maxsize,20,0,60},
15 {maxsize,maxsize,maxsize,maxsize,0}
16 };
17 floyd(A,C);
18 }
19 void floyd(int A[][n],int C[][n]) //A是路径长度矩阵,C是有向网络G的带权邻接矩阵
20 {
21 int i,j,k,next;
22 int max=160;
23 for(i=0;i<n;i++)//设置A和path的初值
24 {
25 for(j=0;j<n;j++)
26 {
27 if(C[i][j]!=max)
28 path[i][j]=j; //j是i的后继
29 else
30 path[i][j]=0;
31 A[i][j]=C[i][j];
32 }
33 }
34 for(k=0;k<n;k++)
35 //做n次迭代,每次均试图将顶点k扩充到当前求得的从i到j的最短路径Pij上
36 {
37 for(i=0;i<n;i++)
38 {
39 for(j=0;j<n;j++)
40 {
41 if(A[i][j]>(A[i][k]+A[k][j]))
42 {
43 A[i][j]=A[i][k]+A[k][j]; //修改长度
44 path[i][j]=path[i][k]; //修改路径
45 }
46 }
47 }
48 }
49 for(i=0;i<n;i++)//输出所有顶点对i,j之间的最短路径Pij的长度及路径
50 {
51 for(j=0;j<n;j++)
52 {
53 if(i!=j)
54 {
55 printf("%d到%d的最短距离为",i+1,j+1);
56 printf("%d\n",A[i][j]); //输出Pij的长度
57 next=path[i][j]; //next为起点i的后继顶点
58 printf("输出路径:\n");
59 if(next==0)
60 printf("%d到%d不可达\n",i+1,j+1);
61 else//Pij存在
62 {
63 printf("%d",i+1);
64 while(next!=j)
65 {
66 printf("——>%d",next+1); //打印后继点
67 next=path[next][j]; //继续找下一个后继点
68 }
69 printf("——>%d\n",j+1); //打印终点
70 }
71 printf("****************************************************\n");
72 }
73 }
74 }
75 }
76
77
78 运行结果:
79 ——所有顶点对之间的最短路径:Floyd算法——
80 (160为无穷远,不可达)
81 1到2的最短距离为10
82 输出路径:
83 1——>2
84 ****************************************************
85 1到3的最短距离为50
86 输出路径:
87 1——>4——>3
88 ****************************************************
89 1到4的最短距离为30
90 输出路径:
91 1——>4
92 ****************************************************
93 1到5的最短距离为60
94 输出路径:
95 1——>4——>3——>5
96 ****************************************************
97 2到1的最短距离为160
98 输出路径:
99 2到1不可达
100 ****************************************************
101 2到3的最短距离为50
102 输出路径:
103 2——>3
104 ****************************************************
105 2到4的最短距离为160
106 输出路径:
107 2到4不可达
108 ****************************************************
109 2到5的最短距离为60
110 输出路径:
111 2——>3——>5
112 ****************************************************
113 3到1的最短距离为160
114 输出路径:
115 3到1不可达
116 ****************************************************
117 3到2的最短距离为160
118 输出路径:
119 3到2不可达
120 ****************************************************
121 3到4的最短距离为160
122 输出路径:
123 3到4不可达
124 ****************************************************
125 3到5的最短距离为10
126 输出路径:
127 3——>5
128 ****************************************************
129 4到1的最短距离为160
130 输出路径:
131 4到1不可达
132 ****************************************************
133 4到2的最短距离为160
134 输出路径:
135 4到2不可达
136 ****************************************************
137 4到3的最短距离为20
138 输出路径:
139 4——>3
140 ****************************************************
141 4到5的最短距离为30
142 输出路径:
143 4——>3——>5
144 ****************************************************
145 5到1的最短距离为160
146 输出路径:
147 5到1不可达
148 ****************************************************
149 5到2的最短距离为160
150 输出路径:
151 5到2不可达
152 ****************************************************
153 5到3的最短距离为160
154 输出路径:
155 5到3不可达
156 ****************************************************
157 5到4的最短距离为160
158 输出路径:
159 5到4不可达
160 ****************************************************
参考:http://blog.sina.com.cn/s/blog_686d0fb001012r05.html
http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html
原文:http://www.cnblogs.com/kunhu/p/3704408.html