Time Limit: 5000/5000 MS
(Java/Others) Memory Limit: 65535/32768 K
(Java/Others)
Total Submission(s): 6674 Accepted
Submission(s): 3112
一个证明需要反向更新的例子:
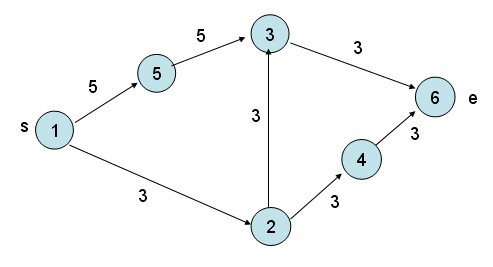
这个图从1到6明显最的流量为3+3=6,但如果不用反向更新,由于用BFS首先找到一条路径1-2-3-6,然后1-2,2-3,3-6这几条边被更新成了0,就再也找不到增广路径到6了,而1-5-3的剩余的5个流量就无路可走了,用反向更新会再在3-2这里加一条流量为3的边,这时候1-5-3的5流量就可以通过这条边到2再到4再到6了,这就是反向更新的需要。
参考:http://blog.csdn.net/huanglianzheng/article/details/5754057
网络最大流入门模板题:
ford fulkerson 标号法:
1 //750MS 4216K 1444 B C++ 2 #include<iostream> 3 #include<queue> 4 #define INF 0x7ffffff 5 #define N 1005 6 using namespace std; 7 int g[N][N],flow[N]; //记录流量fij, 和每次的调整值flow[e] 8 int father[N],vis[N]; //记录父节点 和 标记已遍历节点 9 int maxflow,n,m; 10 inline int Min(int a,int b) 11 { 12 return a<b?a:b; 13 } 14 void ford_fulkerson(int s,int e) 15 { 16 queue<int>Q; 17 maxflow=0; 18 while(1){ //调整到无增广链为止 19 memset(flow,0,sizeof(flow)); 20 memset(vis,0,sizeof(vis)); 21 flow[s]=INF; 22 Q.push(s); 23 while(!Q.empty()){ 24 int u=Q.front(); 25 Q.pop(); 26 for(int v=1;v<=n;v++){ 27 if(!vis[v] && g[u][v]>0){ 28 vis[v]=1; 29 father[v]=u; 30 Q.push(v); 31 flow[v]=Min(flow[u],g[u][v]); 32 } 33 } 34 if(flow[e]>0){ 35 while(!Q.empty()) Q.pop(); 36 break; 37 } 38 } 39 if(flow[e]==0) break; 40 for(int i=e;i!=s;i=father[i]){ 41 g[father[i]][i]-=flow[e]; 42 g[i][father[i]]+=flow[e]; 43 } 44 maxflow+=flow[e]; 45 } 46 } 47 int main(void) 48 { 49 int t,k=1; 50 int a,b,c; 51 scanf("%d",&t); 52 while(t--) 53 { 54 scanf("%d%d",&n,&m); 55 memset(g,0,sizeof(g)); 56 for(int i=0;i<m;i++){ 57 scanf("%d%d%d",&a,&b,&c); 58 g[a][b]+=c; 59 } 60 ford_fulkerson(1,n); 61 printf("Case %d: %d\n",k++,maxflow); 62 } 63 return 0; 64 }
hdu 3549 Flow Problem (网络最大流),布布扣,bubuko.com
原文:http://www.cnblogs.com/GO-NO-1/p/3705093.html