POJ 1673 三角形垂心

Description

Given a triangle ABC, the Extriangles of ABC are constructed as follows:
On each side of ABC, construct a square (ABDE, BCHJ and ACFG in the figure below).
Connect adjacent square corners to form the three Extriangles (AGD, BEJ and CFH in the figure).
The Exomedians of ABC are the medians of the Extriangles, which pass through vertices of the original triangle,extended into the original triangle (LAO, MBO and NCO in the figure. As the figure indicates, the three Exomedians intersect at a common point called the Exocenter (point O in the figure).
This problem is to write a program to compute the Exocenters of triangles.

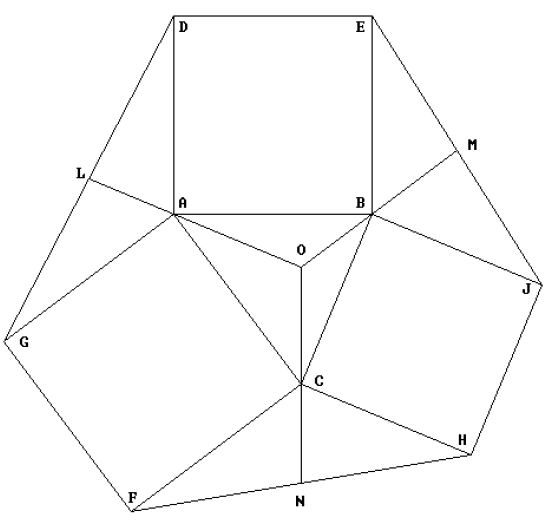
Input

Output

Sample Input

2
0.0 0.0
9.0 12.0
14.0 0.0
3.0 4.0
13.0 19.0
2.0 -10.0

Sample Output

9.0000 3.7500
-48.0400 23.3600

证明过程：

/* ***********************************************
Author :_rabbit
Created Time :2014/5/3 16:37:48
File Name :8.cpp
************************************************ */
#pragma comment(linker, "/STACK:102400000,102400000")
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#include <string>
#include <time.h>
#include <math.h>
#include <queue>
#include <stack>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define eps 1e-8
#define pi acos(-1.0)
typedef long long ll;
struct Point{
	double x,y;
	Point(double _x=0,double _y=0){
		x=_x;y=_y;
	}
};
int dcmp(double x){
	if(fabs(x)<eps)return 0;
	return x<0?-1:1;
}
Point operator + (Point a,Point b){
	return Point(a.x+b.x,a.y+b.y);
}
Point operator - (Point a,Point b){
	return Point(a.x-b.x,a.y-b.y);
}
Point operator * (Point a,double p){
	return Point(a.x*p,a.y*p);
}
Point operator / (Point a,double p){
	return Point(a.x/p,a.y/p);
}
bool operator <(const Point &a,const Point &b){
	return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
bool operator == (const Point &a,const Point  &b){
	return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
}
double Dot(Point a,Point b){
	return a.x*b.x+a.y*b.y;
}
double Length(Point a){
	return sqrt(Dot(a,a));
}
double Angle(Point a,Point b){
	return acos(Dot(a,b)/Length(a)/Length(b));
}
double angle(Point a){
	return atan2(a.y,a.x);
}
double Cross(Point a,Point b){
	return a.x*b.y-a.y*b.x;
}
Point Rotate(Point a,double rad){
	return Point(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad));
}
Point GetLineIntersection(Point p,Point v,Point q,Point w){
	Point u=p-q;
	double t=Cross(w,u)/Cross(v,w);
	return p+v*t;
}
Point perpencenter(Point a,Point b,Point c){
	Point A,B,C,D;
	A=c;
	B.x=c.x-a.y+b.y;
	B.y=c.y+a.x-b.x;
	C=b;
	D.x=b.x-a.y+c.y;
	D.y=b.y+a.x-c.x;
	return GetLineIntersection(A,B-A,C,D-C);
}
int main()
{
     //freopen("data.in","r",stdin);
     //freopen("data.out","w",stdout);
     Point a,b,c;
	 int T;
	 cin>>T;
	 while(T--){
		 cin>>a.x>>a.y>>b.x>>b.y>>c.x>>c.y;
		 Point ans=perpencenter(a,b,c);
		 printf("%.4f %.4f\n",ans.x,ans.y);
	 }
     return 0;
}

POJ 1673 三角形垂心,布布扣,bubuko.com

POJ 1673 三角形垂心

原文：http://blog.csdn.net/xianxingwuguan1/article/details/24929173