Given a complete binary tree, count the number of nodes.
Definition of a complete binary tree from Wikipedia:
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
============
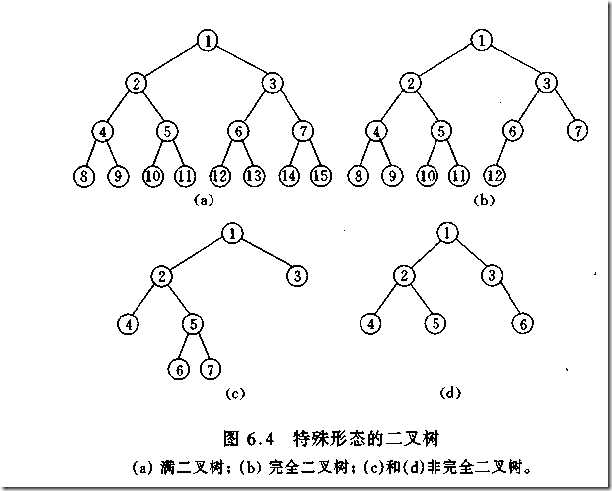
可以证明一个完全二叉树左右子树至少有一个是满二叉树。
满二叉树的节点数是2^k-1,k是树的深度。
所以我们可以先判断该树是否为满二叉树,然后是的话直接返回结果,如果不是递归地求解子树。
这样不用遍历所有的节点。复杂度小于O(N),比对所有点遍历复杂度要小,最好的情况是O(lgN)。
推算大概在O(lgN)~O(N)之间。
具体的分析,取左右子树只有一个是满树的最差情况。
T(N) = lg(N/2) + T(N/2)
T(1) =1
可以推导下复杂度最差在O(lgN*lgN)。
==========
code:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: int countNodes(TreeNode* root) { if(root==nullptr) return 0; TreeNode* lt = root; TreeNode* rt = root; int leftdepth = 0; int rightdepth = 0; while(lt){ leftdepth++; lt = lt->left; } while(rt){ rightdepth++; rt = rt->right; } if(leftdepth==rightdepth) return pow(2,leftdepth)-1; else return countNodes(root->left)+countNodes(root->right)+1; } };
原文:http://www.cnblogs.com/li-daphne/p/5618792.html