In this work, inspired by metric learning based on deep neural features and memory augment neural networks, authors propose matching networks that map a small labelled support set and an unlabelled example to its label. Then they define one-shot learning problems on vision and language tasks and obtain an improving one-shot accuracy on ImageNet and Omnight. The novelty of their work is twofold: at the modeling level, and at the training procedure.
Their non-parametric approach to solving one-shot is based on two components. First, the model architecture follows recent advances in neural networks augmented with memory. Given a support set $S$, the model difines a function $c_S$(or classifier) for each $S$ Sencond, we employ a training strategy which is tailored for one-shot learning from the support set $S$
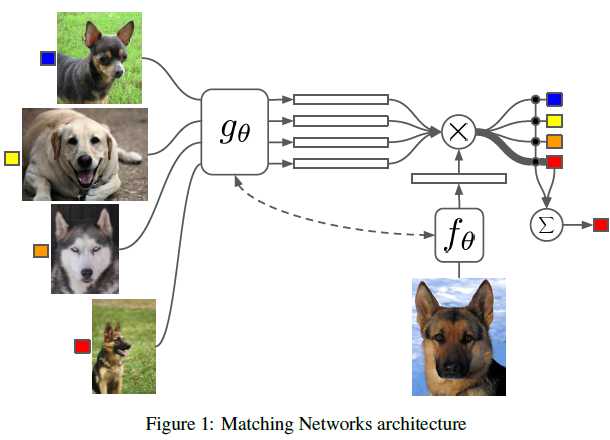
Matching Networks are able to produce sensible test labels for unobserved classes without any changes to the network. We wish to map from a support set of $k$ examples of images-label pairs $S={(x_i,y_i)}_{i=1}^k$ to a classfier $c_S(\hat{x})$ which,given a test example $\hat{x}$, defines a probability distribution over outputs $\hat{y}$. Furthmore, difine the mapping $S\rightarrow c_S(\hat{x})$ to be $P(\hat{y} \mid \hat{x},S)$ where $P$ is parameterised by a neural network. Thus, When given a new support set of examples $S‘$ from which to one-shot learn, we simply use the parametric neural network defined by $P$ to make predictions about the appropriate label $\hat{y}$ for each test example $\hat{x}$: $P(\hat{y} \mid \hat{x},S‘)$. In general, our predicted output class for a given input unseen example $\hat{x}$ and a support set $S$ becomes $arg \max_y P(y\mid \hat{x},S)$. The model in its simplest form computes $\hat{y}$ as follows:
$$ \hat{y}=\sum_{i=1}^k a(\hat{x},x_i)y_i $$
where $x_i,y_i$ are the samples and labels from the support set $S=\{(x_i,y_i)\}_{i=1}^k$, and $a$ is an attention mechanism. Here,the attention kernel function is the softmax over the cosine distance. $$ a(\hat{x},x_i)=\frac{e^{c(f(\hat{x}),g(x_i))}}{\sum_{j=1}^k e^{c(f(\hat{x}),g(x_j))}} $$ where embeding functions $f$ and $g$ are, actually, appropriate neural networks to embed $\hat{x}$ and $x_i$Let us define a tast $T$ as distribution over possible label sets $L$. To form an “episode” to compute gradients and update our model, we first sample $L$ from $T$(e.g.,$L$ could be the label set {cats; dogs}). We then use $L$ to sample the support set $S$ and a batch $B$ (i.e., both $S$ and $B$ are labelled examples of cats and dogs). The Matching Net is then trained to minimise the error predicting the labels in the batch B conditioned on the support set $S$. This is a form of meta-learning since the training procedure explicitly learns to learn from a given support set to minimise a loss over a batch. More precisely, the Matching Nets training objective is as follows:
$$ \theta = arg\max_{\theta}E_{L\sim T}\Big[E_{S\sim L,B\sim L}\Big[\sum_{(x,y)\in B}\log P_{\theta}(y\mid x,S)\Big]\Big] $$
Training $\theta$ with this objective function yields a model which works well when sampling $S‘\sim T‘$ from a different distribution of novel labels
The embedding function for an example $\hat{x}$ in the batch $B$ is as follows:
$$ f(\hat{x},S)=attLSTM(f‘(\hat{x}),g(S),K) $$
where $f‘$ is a neural network. $K$ is the number of "processing" steps following work. $g(S)$ represents the embedding function $g$ applied to each element $x_i$ from the set $S$. Thus, the state after $k$ processing steps is as follows:$$ \hat{h}_k,c_k = LSTM(f‘(\hat{x}),[h_{k-1},r_{k-1}],c_{k-1}) $$
$$ h_k = \hat{h}_k+f‘(\hat{x}) $$
$$ r_{k-1}=\sum_{i=1}^{|S|}a(h_{k-1},g(x_i))g(x_i) $$
$$ a(h_{k-1},g(x_i))=softmax(h_{k-1}^Tg(x_i)) $$
The encoding function for the elements in the support set $S$, $g(x_i,S)$ as a bidirectional LSTM. Let g‘(x_i) be a neural network, then we difine $g(x_i,S)=\vec{h}_i+h_i^{\leftarrow}+g‘(x_i)$ with:
$$ \vec{h}_i,\vec{c}_i=LSTM(g‘(x_i),\vec{h}_{i-1},\vec{c}_{i-1}) $$
$$ h_i^{\leftarrow},c_i^{\leftarrow}=LSTM(g‘(x_i),h_{i+1}^{\leftarrow},c_{i+1}^{\leftarrow}) $$
Reference: https://arxiv.org/abs/1606.04080
Matching Networks for One Shot Learning
原文:http://www.cnblogs.com/huangxiao2015/p/5685293.html