Q:矩阵链乘
熟悉线性代数的同学会知道,矩阵乘法AxB在矩阵A是m x n,矩阵B是n x p的时候才有定义,其运算量是mnp。
那么现在给出n个矩阵,用数组p[](长度为n)来记录各个矩阵的的行列,那么安排一种矩阵乘法的分配方案,使得全局的运算量最少。
分析:很显然这是一个基于线性区间上的一个dp问题,其实dp问题很大的一个难度就在于子问题化,完成了恰到好处的子问题化,递推方程的得到是水到渠成的。而对于线性区间上的问题,子问题的分割往往也是从区间入手。
这里我们的最终解释基于p数组[0,n]的区间段上,我们设置二维数组dp[i][j]用来表示p数组在区间[i-1,j]上的解(也就是第i个矩阵链乘到第j个矩阵的最小运算量),而区间上的dp最常见的子问题化就是定义好状态之后,取一点,然后然这个点遍历[i,j]区间来得到所有的子问题然后维护最值便可完成整个dp过程。
其实也可以理解为,枚举区间[i,j]上最后一次链乘的中间参数k的所有位置。
在这里,为了求解dp[i][j],我们设置区间k∈(i,j),那么很容易得到如下的状态转移方程:
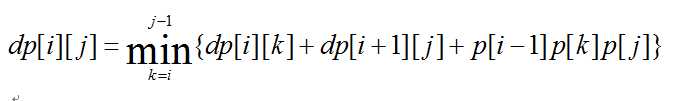
边界情况:dp[i][i] = 0.
原文:http://www.cnblogs.com/rhythmic/p/5693214.html