对于一个合格的程序员来说,掌握一定的数学知识是非常必要的,所以这次就开个数学专题玩玩。
不多说啥,上题目,我们直接分析题目!
首先ORZ stonepage神犇,一眼就看出我把快速幂写成快速乘了……
话说%2007为啥不是2007年的题?还TMD是市选,MDZZ;
算了不管他,我们说我们的:
由于题目要求一个生成树,那么我们就要保证所有的点在一个联通块里面,so,怎么做呢?
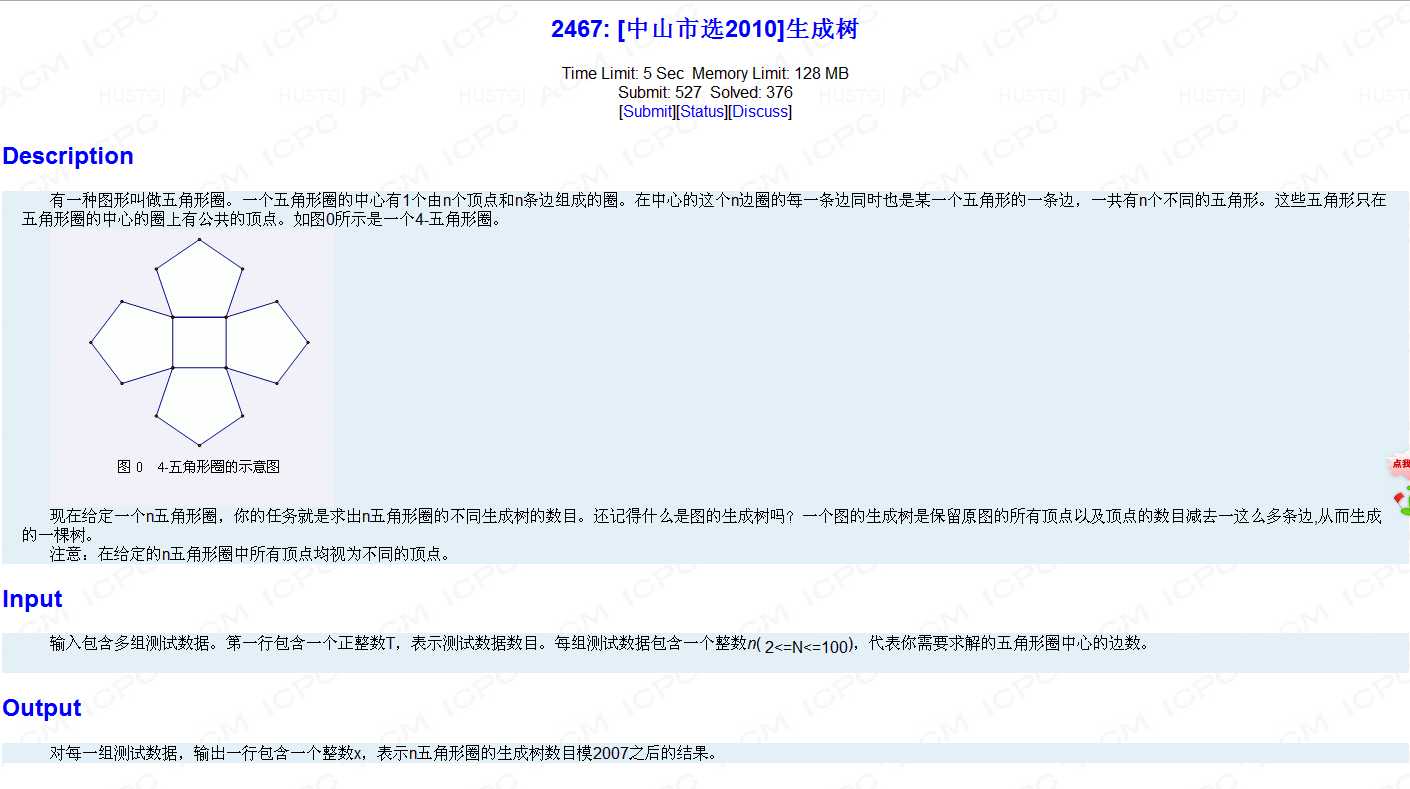
首先观察这一个图,我们很容易能发现,其实我们只需要删去n+1条边,那么怎么删呢?
首先外围的五边形只能每个最少删去一条边这样一共才刚刚删掉n条边。
所以我们肯定要在中心n边形上删去一条边。由于中心n边形的每条边都是所有五边形中的一条边,所以呢就相当于有一个五边形要删掉2条边。
手动枚举删掉两条边的五边形,发现这个五边形一共有4种删边方法。
对于剩下的删除一条边五边形们,就一共有5的n-1次方种删除方法。
由于中心多边形是n条边,所以我们要的方案总数就是ans = 5^(n-1) ×4×n种,然后%p就可以啦;
什么,你不知道怎么算?这个就是个快速幂的基本套路……
接下来上代码啦,发福利啦:
1 #include <iostream> 2 #include <cstdio> 3 #include <cmath> 4 #include <algorithm> 5 #include <cstring> 6 #include <cstdlib> 7 using namespace std; 8 int get_num(){ 9 int num = 0; 10 bool flag = false; 11 char c; 12 while((c = getchar()) == ‘ ‘ || c == ‘\n‘ || c == ‘\r‘); 13 if(c == ‘ ‘)flag = true; 14 else num = c - ‘0‘; 15 while(isdigit(c = getchar())) 16 num = num * 10 + c - ‘0‘; 17 return (flag ? -1 : 1)*num; 18 } 19 int quick_pow(int x,int y,int p){ 20 int ans = 1; 21 for(;y;x = (x*x) % p,y >>= 1) 22 if(y & 1){ 23 ans = (ans * x)%p; 24 } 25 return ans; 26 } 27 int n,m,T,p = 2007; 28 int main(){ 29 T = get_num(); 30 while(T--){ 31 n = get_num(); 32 int ans; 33 ans = 4 * quick_pow(5,n-1,p) * (n%p); 34 ans %= p; 35 printf("%d\n",ans); 36 } 37 return 0; 38 } 39 /* 40 srO stonepage orz; 41 */
如果有什么意见,请留言我的邮箱PC-worker@outlook.com,谢谢。
原文:http://www.cnblogs.com/gangding/p/5719746.html