在数轴上有 nn 个闭区间 2],...,[ln[l1,r1],[l2,r2],...,[ln,rn]。现在要从中选出 mm 个区间,使得这 mm 个区间共同包含至少一个位置。换句话说,就是使得存在一个 xx,使得对于每一个被选中的区间 [li,ri][li,ri],都有 li≤x≤rili≤x≤ri。
对于一个合法的选取方案,它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 i,ri][li,ri] 的长度定义为 ri−liri−li,即等于它的右端点的值减去左端点的值。
求所有合法方案中最小的花费。如果不存在合法的方案,输出 −1−1。
第一行包含两个正整数 n,mn,m,用空格隔开,意义如上文所述。保证 1≤m≤n1≤m≤n。
接下来 nn 行,每行表示一个区间,包含用空格隔开的两个整数 lili 和 riri 为该区间的左右端点。
只有一行,包含一个正整数,即最小花费。
6 3 3 5 1 2 3 4 2 2 1 5 1 4
2
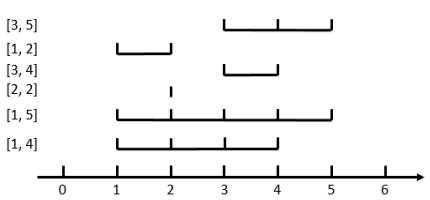
如图,当 n=6, m=3n=6, m=3 时,花费最小的方案是选取 [3,5][3,5]、[3,4][3,4]、[1,4][1,4] 这三个区间,他们共同包含了 44 这个位置,所以是合法的。其中最长的区间是 [1,4][1,4],最短的区间是 [3,4][3,4],所以它的花费是 (4−1)−(4−3)=2(4−1)−(4−3)=2。
见样例数据下载。
见样例数据下载。
所有测试数据的范围和特点如下表所示:
| 测试点编号 | nn | mm | li,rili,ri |
|---|---|---|---|
| 1 | 2020 | 99 | 0≤li≤ri≤1000≤li≤ri≤100 |
| 2 | 1010 | ||
| 3 | 199199 | 33 | 0≤li≤ri≤1000000≤li≤ri≤100000 |
| 4 | 200200 | ||
| 5 | 10001000 | 22 | |
| 6 | 20002000 | ||
| 7 | 199199 | 6060 | 0≤li≤ri≤50000≤li≤ri≤5000 |
| 8 | 200200 | 5050 | |
| 9 | 0≤li≤ri≤1090≤li≤ri≤109 | ||
| 10 | 19991999 | 500500 | 0≤li≤ri≤50000≤li≤ri≤5000 |
| 11 | 20002000 | 400400 | |
| 12 | 500500 | 0≤li≤ri≤1090≤li≤ri≤109 | |
| 13 | 3000030000 | 20002000 | 0≤li≤ri≤1000000≤li≤ri≤100000 |
| 14 | 4000040000 | 10001000 | |
| 15 | 5000050000 | 1500015000 | |
| 16 | 100000100000 | 2000020000 | |
| 17 | 200000200000 | 0≤li≤ri≤1090≤li≤ri≤109 | |
| 18 | 300000300000 | 5000050000 | |
| 19 | 400000400000 | 9000090000 | |
| 20 | 500000500000 | 200000200000 |
时间限制:3S
空间限制:128M
正解:离散化+线段树维护+决策单调性
解题报告:
NOI2016day2T1,考场上写了个复杂度跟长度有关的算法,期望得分只有50分。
实际上我想的就是正解了,然而我没有想到优化。实际上区间显然可以离散化,多余部分可以不要,只需要考虑(视为)端点相交即可,也就是中间没有端点的部分直接缩成一个点就可以了。
考虑答案一定是将区间按长度排序后连续的一段(我暴力里面用了这个思想,mdzz),也就是说具有决策单调性。所以我们只需要快速维护整个区间内被覆盖的最大次数(点被覆盖)。显然线段树直接维护即可。
1 //It is made by jump~ 2 #include <iostream> 3 #include <cstdlib> 4 #include <cstring> 5 #include <cstdio> 6 #include <cmath> 7 #include <algorithm> 8 #include <ctime> 9 #include <vector> 10 #include <queue> 11 #include <map> 12 #include <set> 13 #ifdef WIN32 14 #define OT "%I64d" 15 #else 16 #define OT "%lld" 17 #endif 18 using namespace std; 19 typedef long long LL; 20 const int MAXN = 500011; 21 int n,m,cnt,L,ql,qr,val; 22 int p[MAXN*4],ans; 23 struct cha{ 24 int l,r,len; 25 }Q[MAXN]; 26 27 struct node{ 28 int lazy,maxl; 29 }a[MAXN*8]; 30 31 inline int getint() 32 { 33 int w=0,q=0; 34 char c=getchar(); 35 while((c<‘0‘ || c>‘9‘) && c!=‘-‘) c=getchar(); 36 if (c==‘-‘) q=1, c=getchar(); 37 while (c>=‘0‘ && c<=‘9‘) w=w*10+c-‘0‘, c=getchar(); 38 return q ? -w : w; 39 } 40 41 inline bool cmp(cha q,cha qq){ return q.len<qq.len; } 42 43 inline void pushdown(int root,int l,int r){ 44 if(!a[root].lazy) return ; 45 int lc=root*2,rc=lc+1; 46 a[lc].lazy+=a[root].lazy; a[rc].lazy+=a[root].lazy; 47 a[lc].maxl+=a[root].lazy; a[rc].maxl+=a[root].lazy; 48 a[root].lazy=0; 49 } 50 51 inline void update(int root,int l,int r){ 52 if(ql<=l && r<=qr) { a[root].lazy+=val; a[root].maxl+=val; return ; } 53 pushdown(root,l,r); 54 int mid=(l+r)/2; int lc=root*2,rc=lc+1; 55 if(ql<=mid) update(lc,l,mid); if(qr>mid) update(rc,mid+1,r); 56 a[root].maxl=max(a[lc].maxl,a[rc].maxl); 57 } 58 59 inline void work(){ 60 n=getint(); m=getint(); for(int i=1;i<=n;i++) Q[i].l=getint(),Q[i].r=getint(),p[++cnt]=Q[i].l,p[++cnt]=Q[i].r,Q[i].len=Q[i].r-Q[i].l; 61 sort(p+1,p+cnt+1); 62 L=unique(p+1,p+cnt+1)-p-1; 63 for(int i=1;i<=n;i++) Q[i].l=lower_bound(p+1,p+L+1,Q[i].l)-p,Q[i].r=lower_bound(p+1,p+L+1,Q[i].r)-p;//离散化 64 int now=0; sort(Q+1,Q+n+1,cmp); 65 ans=(1<<30); 66 for(int i=1;i<=n;i++) {//决策单调性,一定是连续区间 67 while(a[1].maxl<m) { 68 if(now==n) return ; 69 now++; val=1; ql=Q[now].l; qr=Q[now].r; 70 update(1,1,L); 71 } 72 ans=min(Q[now].len-Q[i].len,ans); 73 ql=Q[i].l; qr=Q[i].r; val=-1; 74 update(1,1,L); 75 } 76 } 77 78 int main() 79 { 80 work(); 81 if(ans==(1<<30)) ans=-1; 82 printf("%d",ans); 83 return 0; 84 }
原文:http://www.cnblogs.com/ljh2000-jump/p/5730451.html