定义掌握：
单个样本的t检验
目的：比较样本均数 所代表的未知总体均数μ和已知总体均数μ0。
计算公式：
t统计量：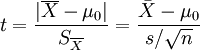
自由度：v=n - 1
适用条件：
(1) 已知一个总体均数；
(2) 可得到一个样本均数及该样本标准误；
(3) 样本来自正态或近似正态总体。
T检验的步骤
1、建立虚无假设H0:μ1 = μ2，即先假定两个总体平均数之间没有显著差异；
2、计算统计量t值，对于不同类型的问题选用不同的统计量计算方法；
1）如果要评断一个总体中的小样本平均数与总体平均值之间的差异程度，其统计量t值的计算公式为：
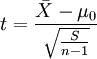
2）如果要评断两组样本平均数之间的差异程度，其统计量t值的计算公式为：
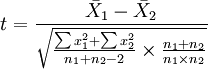
3、根据自由度df=n-1，查t值表，找出规定的t理论值并进行比较。理论值差异的显著水平为0.01级或0.05级。不同自由度的显著水平理论值记为t(df)0.01和t(df)0.05
4、比较计算得到的t值和理论t值，推断发生的概率，依据下表给出的t值与差异显著性关系表作出判断。
| T值与差异显著性关系表 | ||
|---|---|---|
| t | P值 | 差异显著程度 |
 |
 |
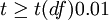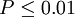差异非常显著 |
 |
 |
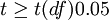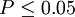差异显著 |
| t < t(df)0.05 | P > 0.05 | 差异不显著 |
5、根据是以上分析，结合具体情况，作出结论。
与通常的统计推断问题一样，方差分析的任务也是先根据实际情况提出原假设H0与备择假设H1，然后寻找适当的检验统计量进行假设检验。本节将借用上面的实例来讨论单因素试验的方差分析问题。
在上例中，因素A（即抗生素）有s（=5）个水平
，在每一个水平
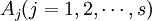下进行了nj =
4次独立试验，得到如上表所示的结果。这些结果是一个随机变量。表中的数据可以看成来自s个不同总体（每个水平对应一个总体）的样本值，将各个总体的均值依次记为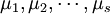
,则按题意需检验假设
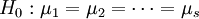
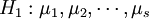不全相等
为了便于讨论，现在引入总平均μ
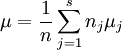其中：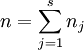
再引入水平Aj的效应δj
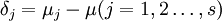
显然有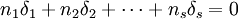
，δj表示水平Aj下的总体平均值与总平均的差异。
利用这些记号，本例的假设就等价于假设
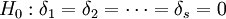
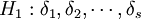不全为零
因此，单因素方差分析的任务就是检验s个总体的均值μj是否相等，也就等价于检验各水平Aj的效应δj是否都等于零。
2. 检验所需的统计量
假设各总体服从正态分布，且方差相同，即假定各个水平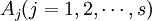下的样本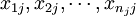
来自正态总体N(μj,σ2)，μj与σ2未知，且设不同水平Aj下的样本之间相互独立，则单因素方差分析所需的检验统计量可以从总平方和的分解导出来。下面先引入：
水平Aj下的样本平均值:
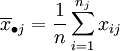
数据的总平均:
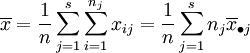
总平方和:
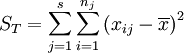
总平方和ST反映了全部试验数据之间的差异，因此ST又称为总变差。将其分解为
ST = SE + SA
其中:
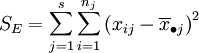
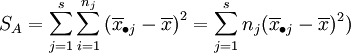
上述SE的各项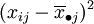
表示了在水平Aj下，样本观察值与样本均值的差异，这是由随机误差所引起的，因此SE叫做误差平方和。SA的各项
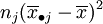表示了在水平Aj下的样本平均值与数据总平均的差异，这是由水平Aj以及随机误差所引起的，因此SA叫做因素A的效应平方和。
可以证明SA与SE相互独立，且当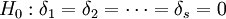为真时，SA与SE分别服从自由度为s ?
1,n ? s的χ2分布，即
SA / σ2?χ2(s ? 1)
SE / σ2?χ2(n ? s)
于是，当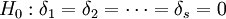为真时
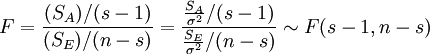
这就是单因素方差分析所需的服从F分布的检验统计量。
3. 假设检验的拒绝域
通过上面的分析可得，在显著性水平α下，本检验问题的拒绝域为
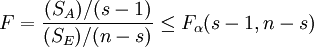
为了方便分析比较，通常将上述分析结果编排成如下表所示的方差分析表。表中的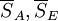
分别称为SA,SE的均方。
| 方差来源 | 平方和 | 自由度 | 均方 | F比 |
| 因素A | SA | s ? 1 |  |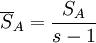
 |
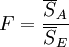| 误差 | SE | n ? s |  |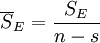
|
| 总和 | ST | n ? 1 |
假设检验是围绕对原假设内容的审定而展开的。如果原假设正确我们接受了（同时也就拒绝了备择假设），或原假设错误我们拒绝了（同时也就接受了备择假设），这表明我们作出了正确的决定。但是，由于假设检验是根据样本提供的信息进行推断的，也就有犯错误的可能。有这样一种情况，原假设正确，而我们却把它当成错误的加以拒绝。犯这种错误的概率用α表示，统计上把α称为假设检验中的显著性水平，，也就是决策中所面临的风险。
显著性水平是假设检验中的一个概念，是指当原假设为正确时人们却把它拒绝了的概率或风险。它是公认的小概率事件的概率值，必须在每一次统计检验之前确定，通常取α＝0.05或α＝0.01。这表明，当作出接受原假设的决定时，其正确的可能性（概率）为95％或99％。
显著性水平代表的意义是在一次试验中小概率事物发生的可能性大小。
原文：http://www.cnblogs.com/wangwp/p/3714669.html