边界:感知
在逻辑回归中,$p(y=1 \mid x;\theta)$的概率由$h_{\theta}(x)=g(\theta^{T}x)$建立模型。当$h_{\theta}(x)\geq 0.5$则预测x的输出为1。或者说当$\theta_{x} \geq 0$则预测x的输出为1。因此当$\theta_{x} \gg 0$时,我们认为准确预测输出为1。
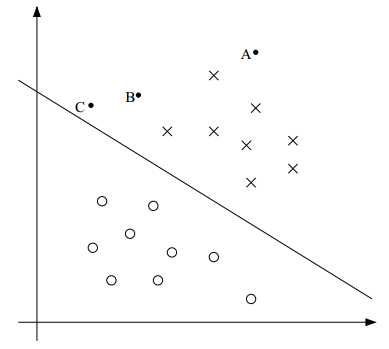
如上图,点A可以准确预测为x,而C点距离判决边界太近,无法做出准确预测。因此,我们希望找到一个判决边界,使得基于训练样本可以做出准确预测。
标记
为了更方便的讨论SVM,引入新的标记方法。对于二分类问题中的标签y和特征x,我们令$y \in {-1,1}$来表示类的标签,不像之前的线性分类器那样使用$\theta$向量,这里使用参数$w,b$,分类器如下:
$h_{w,b}(x)=g(w^{T}x+b)$
式中的$b$相当于之前的$\theta_{0}$,$w$相当于$[\theta_{1},...,\theta_{n}]^{T}$。并且当$z \geq 0$时有$g(z)=1$,$z < 0$时有$g(z)=0$
函数和几何边界
定义$(w,b)$的函数边界:
$\hat {\gamma }^{(i)}=y^{(i)}(w^{T}x+b) $
如果$y^{(i)}=1$,若要函数边界较大,则需要$w^{T}x+b$是一个较大的正数。
对于以上给出的$g$,当我们将$w$变为$2w$,$b$变为$2b$时,$g(w^{T}x+b)$变为$g(2w^{T}x+2b)$,这并不会改变$h_{w,b}(x)$,因为其取决于$w^{T}x+b$的符号而不是幅度。因此我们可以任意的增大函数边界。
直观来看,引入一些正则化条件可能是有意义的,比如$\left \| w \right \|_{2}=1$,则$(w,b)$变为$(w/\left \| w \right \|_{2},b/\left \| w \right \|_{2})$。
给定训练集$S={(x^{(i)},y^{(i)});i=1,...,m}$,对独立的样本定义关于$(w,b)$的在$S$中最小的边界函数(个人理解是所有样本点到判决边界的最小距离):
$\hat {\gamma } = \underset{i=1,...,m}{min}\hat {\gamma }^{(i)}$
接下来讨论几何边界:
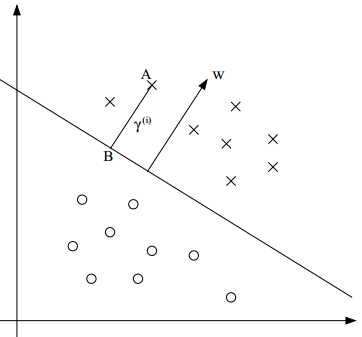
如上图,$(w,b)$对应的判决边界如图所示。$w$与分割超平面正交。A点代表标签为$y^{(i)}=1$的$x^{(i)}$的输入,该点到判决边界的距离为$\gamma^{(i)}$,以线段AB表示。
那么如何计算$\gamma^{(i)}$的值呢?$w/||w||$是与w同方向的一个单位向量。既然A点表示$x^{(i)}$,那么我们可以发现B点可以由$x^{(i)}-\gamma^{(i)} \cdot w/||w||$表示,示意图如下:
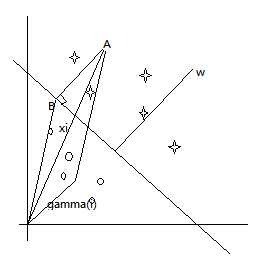
对于所有在判决边界上的点x都有$w^{T}x+b=0$,因此:
$W^{T}(x^{(i)}-\gamma^{(ii)}\frac{w}{||w||})+b=0$
解得:
$w^{T}(x^{(i)}-\gamma^{(i)} \frac{w}{||2||})+b=0$
$w^{T}x^{(i)}+b=w^{T}\gamma^{(i)} \frac{w}{||w||}$
因为$v^{(i)}$是一个数值,$w$是一个列向量,则:
$w^{T}x^{(i)}+b=\gamma^{(i)} w^{T}\frac{w}{||w||}$
$w^{T}x^{(i)}+b=\gamma^{(i)} ||w||$
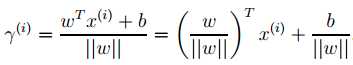
这是A点在y=1的一侧时的计算结果,更通用的公式如下:
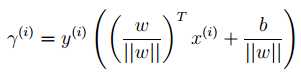
最优边界分类器
原文:http://www.cnblogs.com/wuchaodzxx/p/5738446.html