[BZOJ3771]Triple
试题描述
输入
输出
输入示例
4 4 5 6 7
输出示例
4 1 5 1 6 1 7 1 9 1 10 1 11 2 12 1 13 1 15 1 16 1 17 1 18 1
数据规模及约定
所有数据满足：Ai<=40000
题解
这题用了一个叫母函数的东西。其实就是搞一个多项式 A，其中第 xi 的系数为数字 i 的出现次数，那么容易发现两个 A 相乘可以得到两个数加和组成的每一个数不考虑顺序和重复的方法，具体来说设两个数加起来和为 n 的方案为 Bn ，数 n 的出现次数为 An 则有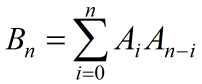
，容易发现这是个卷积的形式，所以是两个多项式 A 相乘。注意需要排除重复和顺序不当的情况，所以还需要设置一个多项式 A2，其中第 xi 表示 i/2 的出现次数，那么 (A*A-A2)/2 就是两个数加起来考虑顺序和重复的方案数了。同理三个数的也可以自己yy一下推出来。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <queue>
#include <cstring>
#include <string>
#include <map>
#include <set>
using namespace std;
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
int read() {
int x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = Getchar(); }
return x * f;
}
#define maxn 240010
#define LL long long
const double pi = acos(-1.0);
struct Complex {
double a, b;
Complex() { a = b = 0.0; }
Complex operator + (const Complex& t) const {
Complex ans;
ans.a = a + t.a;
ans.b = b + t.b;
return ans;
}
Complex operator += (const Complex& t) {
*this = *this + t;
return *this;
}
Complex operator - (const Complex& t) const {
Complex ans;
ans.a = a - t.a;
ans.b = b - t.b;
return ans;
}
Complex operator * (const Complex& t) const {
Complex ans;
ans.a = a * t.a - b * t.b;
ans.b = a * t.b + b * t.a;
return ans;
}
Complex operator * (const double& t) const {
Complex ans;
ans.a = a * t;
ans.b = b * t;
return ans;
}
Complex operator *= (const Complex& t) {
*this = *this * t;
return *this;
}
} A[maxn], A2[maxn], A3[maxn], ans[maxn];
int n, m;
int Ord[maxn];
void FFT(Complex a[], int n, int tp) {
for(int i = 0; i < n; i++) if(i < Ord[i]) swap(a[i], a[Ord[i]]);
for(int i = 1; i < n; i <<= 1) {
Complex w, wn; wn.a = cos(pi / i); wn.b = sin(pi / i) * tp;
for(int j = 0; j < n; j += (i << 1)) {
w.a = 1.0; w.b = 0.0;
for(int k = 0; k < i; k++) {
Complex t1 = a[j+k], t2 = w * a[j+k+i];
a[j+k] = t1 + t2;
a[j+k+i] = t1 - t2;
w *= wn;
}
}
}
if(tp < 0) for(int i = 0; i <= n; i++) a[i].a = (int)(a[i].a / n + .5);
return ;
}
int main() {
int t = read();
for(int i = 1; i <= t; i++) {
int x = read();
A[x].a += 1.0; A2[x<<1].a += 1.0; A3[x*3].a += 1.0;
n = max(n, x);
}
m = n * 3; int L = 0;
for(n = 1; n <= m; n <<= 1) L++;
for(int i = 0; i < n; i++) Ord[i] = (Ord[i>>1] >> 1) | ((i & 1) << L - 1);
FFT(A, n, 1); FFT(A2, n, 1); FFT(A3, n, 1);
for(int i = 0; i <= n; i++) ans[i] = A[i] + (A[i] * A[i] - A2[i]) * .5 + (A[i] * A[i] * A[i] - A[i] * A2[i] * 3.0 + A3[i] * 2.0) * (1.0 / 6.0);
FFT(ans, n, -1);
for(int i = 1; i <= m; i++) if((int)ans[i].a)
printf("%d %d\n", i, (int)ans[i].a);
return 0;
}
原文：http://www.cnblogs.com/xiao-ju-ruo-xjr/p/5739987.html