
上一章的内容中介绍到非线性的SVM可以利用一个不大的VC dimension来刻画比较复杂的边界。但是如果当这个VC dimension变得比较大的时候,计算就比较费时了。
这一章将会介绍非线性SVM的另一种理解和解决方法。

在这里,我们将左边的约束条件转化成为利用拉格朗日乘数法表示成为右边的式子,接下去证明右边的式子可以完全表示出左边的约束条件
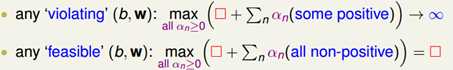
当yn(wTzn+b)>=1时,max之后的表达式就可以得到一个收敛的值。
相反,当yn(wTzn+b)<1时,max之后的表达式就会发散到正无穷。
因此,我们通过这个max的求解过程就可以把之前的约束条件包含了进来。

这里,交换了min和max的次序,得到了之前式子的一个下界限,事实上,如果求解的问题满足强对偶的三个条件,左边的式子可以和右边的式子等同起来,这三个条件就是
1. 凸函数
2. 问题是有解的(对应到SVM这里要解决的问题就是两类点可以被直线或曲线区分开来)。
3. 约束条件是线性的。
所以最后可以找到同一组的解(b,w,a)对左边和右边的式子同样适用。
所以问题就转换成为如下的形式
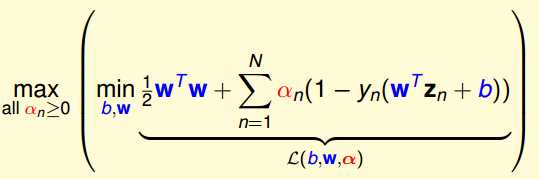
这样处理的好处就是我们将一个先处理an的问题转化成为了一个先处理b和w的优化问题。

先对b进行求导,那么得到一个约束条件,然后把它代进去,可以消去一项
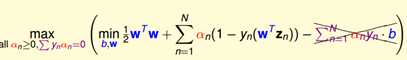
再对w进行求导,那么得到一个约束条件,然后把它代进去,可以化简

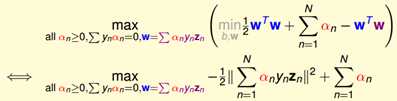
KKT条件:
最后,求解的问题化简成为的形式如下:
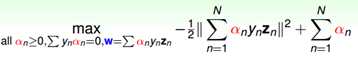
这里有一个KKT条件(只有满足KKT条件的情况下,上述问题才有解)

这里最后一个条件尤为重要,在最优解的时候,要有最优解存在,那么就要使得an=0或者后面的一项等于0,这样拉格朗日项才会消去。
于是,最终我们就可以用下面的式子对最优的an进行求解。目前该问题中就包含了N个变量,N+1个约束。

接下来就是利用QP Solver 求解问题的过程了。这里略去。
这里需要注意到的问题是当前的问题规模是由进行训练的数据集大小决定的,当进行训练的数据很大的时候QP Solver解问题的过程就很慢了。所以最好使用专门为SVM设计的Solver进行问题的求解。

我们得到了an,之后就可以利用KKT条件,对w,b进行求解,上图方框中的式子就可以得到w,之后我们利用primal-inner条件,如果an不为0,那么后面的一项就可以解出来了,事实上,当an>0的时候,这些点就是落在margin 边界上的那些点。

所以我们在求解的时候只是用到了在边界上的那些点,对于不在边界上的点都没有采用,SV去计算w和b的时候也是只有采用了在边界上的那些点。

对比SVM和PLA,我们都是使用了zn来表示w,所以w是由训练使用的数据来表示的,只是SVM只用到了落在边界上的SV来表示w。

对比两种SVM的求解方式,当训练的数据量比较少的时候,我们可以采用Dual SVM,当数据的边界不太复杂,VC dimension不高的时候我们可以采用Primal SVM的方式。

但是,最终我们希望在求解SVM问题的时候,我们不希望考虑 VC dimension的维度,但是采用Dual SVM的时候,我们在qn,m中还是使用了zn,zm,这种受到VD dimension约束的数据,所以接下去会讲到不受VC dimension约束的求解方法。
原文:http://www.cnblogs.com/enzyme/p/5742966.html