这一章节我们主要讨论定义在R^n空间上的向量之间的关系,而这个关系概括来讲其实就是正交,然后引入正交投影、最佳逼近定理等,这些概念将为我们在求无解的线性方程组Ax=b的最优近似解打下基石.
正交性:
先举个最简单的例子,在平面中,两个二维向量的点乘如果为0,那么我们可判定两个向量互相垂直,那么实际上这两个向量就是R^2向量空间上的一组正交向量。
下面推广到R^n向量空间上,给出正交性的定义:
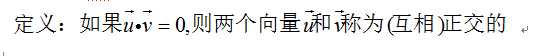
正交集:
给定向量集合S,当S中任意两个元素都相互正交,我们称S是一个正交集。

基的一个概念其实表征一个空间(集合)中所有元素的一些分量,它的概念和线性无关紧密联系的,所以这里我们将实现放在线性无关上即可。


这个定理其实就显现出了对于子空间W,用正交基相对于用其他非正交基的优势,它在计算权值上有着极大的便利性,给出子空间W中某个向量y,我们便可以它基于正交基的线性表示。
这样计算的正确性的证明也很好证明,充分利用正交这一条性质即可。

《Linear Algebra and Its Applications》-chaper6正交性和最小二乘法-正交性
原文:http://www.cnblogs.com/rhythmic/p/5797188.html