There are two sorted arrays A and B of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
第一次看到的时候做不出来,看了答案之后到今天重做,还是不会。
整体思路就是把求中位数转换为求在两个sorted array里求第k个数。如果(m+n)%2=0,那么就是求第m + n) / 2和第m + n) / 2 + 1个数的平均数。
如果(m+n)%2!=0,那么就是求第m + n) / 2 + 1个数。
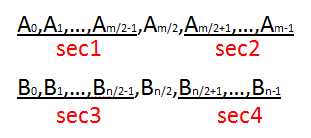
如图,如果m/2+n/2+1>=k的时候,那么第k个数一定是在sec1,sec3之中或者A[m/2],A[n/2]。此时如果A[m/2]>=B[n/2],那么第k个数一定不在sec2中。(因为在sec2中的数已经比sec1和sec3都大了。)如果A[m/2]<B[n/2],那么第k个数一定不在sec4中。
如果m/2+n/2+1<k,那么第k个数不可能在sec1或者sec3中。如果A[m/2]<B[n/2],那么第k个数一定不在sec1。如果A[m/2]>=B[n/2],第k个数一定不在sec3。
当m=0时,也就是A为空,那么第k个数一定是B的第一个。n=0同理。
当k=1时,也就是说第一个数,那么就是两个sorted array第一个项的最小值。
1 class Solution { 2 public: 3 double findMedianSortedArrays(int A[], int m, int B[], int n) { 4 if ((m + n) %2 == 0) { 5 return (getKthNum(A, m, B, n, (m + n) / 2) + getKthNum(A, m, B, n, (m + n) / 2 + 1)) / 2.0; 6 } else { 7 return getKthNum(A, m, B, n, (m + n) / 2 + 1); 8 } 9 } 10 11 int getKthNum(int A[], int m, int B[], int n, int k) { 12 if (m <= 0) return B[k - 1]; 13 if (n <= 0) return A[k - 1]; 14 if (k <= 0) return min(A[0], B[0]); 15 16 if (m / 2 + n / 2 + 1 >= k) { 17 if (A[m / 2] >= B[n / 2]) { 18 return getKthNum(A, m / 2, B, n, k); 19 } else { 20 return getKthNum(A, m, B, n / 2, k); 21 } 22 } else { 23 if (A[m / 2] >= B[n / 2]) { 24 return getKthNum(A, m, B + n / 2 + 1, n - n / 2 - 1, k - n / 2 - 1); 25 } else { 26 return getKthNum(A + m / 2 + 1, m - m / 2 - 1, B, n, k - m / 2 - 1); 27 } 28 } 29 } 30 };
Leetcode | Median of Two Sorted Arrays,布布扣,bubuko.com
Leetcode | Median of Two Sorted Arrays
原文:http://www.cnblogs.com/linyx/p/3718684.html