我发现,想要了解一个领域的比较快速的方法就是去读本领域近几年的硕士和博士毕业论文(中文的就行)!
拉格朗日对偶
今天学习了拉格朗日对偶。我们首先考虑下面这个问题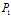 :
:
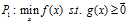
我们记
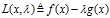
(这里如果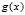 是一个向量的话,那么相应的
是一个向量的话,那么相应的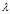 也是一个向量),则上述最优化问题可以等价于问题
也是一个向量),则上述最优化问题可以等价于问题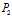 :
:
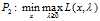
于是我们现在似乎可以开始求解问题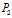 了,最通常的求解过程就是先找到
了,最通常的求解过程就是先找到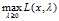 的最优解
的最优解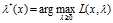 ,次最优解显然是
,次最优解显然是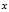 的函数,然后将这个最优解
的函数,然后将这个最优解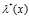 带入问题
带入问题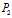 继续求
继续求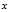 的最优解
的最优解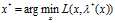 ,就可以得到问题
,就可以得到问题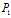 的最优解为
的最优解为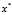 。但是,通过这种方法来求解其实和直接求解
。但是,通过这种方法来求解其实和直接求解 是一样的(本段结束后举个例子来说明)。于是,我们可以使用一个称为"对偶"的思想来解决这个问题。部分解决。
是一样的(本段结束后举个例子来说明)。于是,我们可以使用一个称为"对偶"的思想来解决这个问题。部分解决。
下面举个例子来说明,假设我们想求解问题:
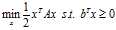 ,
,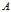 是一个方阵
是一个方阵
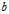 是一个向量
是一个向量
那么它的等价形式是
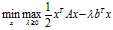
我们首先求解max,结果如下:
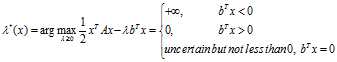
带入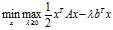 可得:
可得:
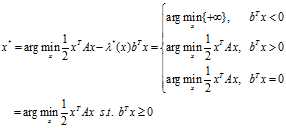
这等价于原问题,相当于什么忙都没帮上,还是回到了原点。
下面我们介绍拉格朗日对偶来处理此问题。我们定义"拉格朗日对偶函数"为:
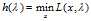
相应的"拉格朗日对偶问题"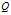 定义为:
定义为:
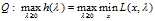
我们可以立刻得到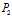 与
与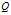 之间的关系,当
之间的关系,当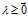 且
且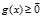 时我们有
时我们有
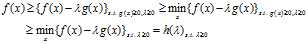
上面的第三个不等式是由于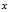 的取值范围从
的取值范围从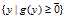 扩大到了
扩大到了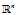 ,大范围内的最小值肯定大于小范围内的最小值。这一点很关键!因为正是由于这个原因,可以把"
,大范围内的最小值肯定大于小范围内的最小值。这一点很关键!因为正是由于这个原因,可以把"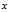 必须满足
必须满足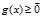 "这个条件从限制条件中去除掉。这是一个比"
"这个条件从限制条件中去除掉。这是一个比"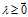 "难处理的条件,去掉它当然有很大的益处。从上式中我们得到:
"难处理的条件,去掉它当然有很大的益处。从上式中我们得到:
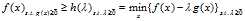
于是更进一步,我们有下式:
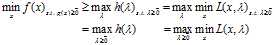
而我们一开始就提到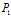 等价于
等价于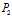 ,那么将
,那么将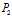 带入便可得到:
带入便可得到:
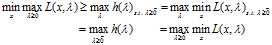
可得:
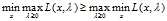
我们发现现在所有对自变量的约束仅剩下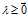 ,而
,而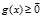 这个约束条件不见了,如果我们能使得的等号成立,那么我们就可以得到更好的结果。我们考虑如下可能:如果能够取等,并且关于
这个约束条件不见了,如果我们能使得的等号成立,那么我们就可以得到更好的结果。我们考虑如下可能:如果能够取等,并且关于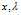 的两组最优解(
的两组最优解(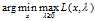 和
和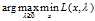 )也相等的话,那么我们可以通过交换max和min的求解顺序来求解最初的问题。因为
)也相等的话,那么我们可以通过交换max和min的求解顺序来求解最初的问题。因为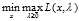 通常是难解的,所以我们便可以通过这种办法转化为去求解
通常是难解的,所以我们便可以通过这种办法转化为去求解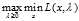 。假设
。假设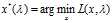 ,我们将
,我们将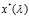 带入
带入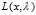 得打
得打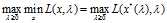 ,再求解
,再求解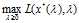 得到
得到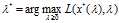 ,于是的最优解便是
,于是的最优解便是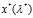 。
。
补充一下,当然我们也可以通过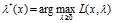 然后
然后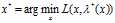 的方法来求最优解
的方法来求最优解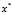 ,不过这样就相当于直接求解
,不过这样就相当于直接求解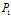 的等价命题
的等价命题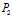 ,上面我已经谈论过这条路是个死胡同了,因此先求max再求min是行不通的,只能先min后max。
,上面我已经谈论过这条路是个死胡同了,因此先求max再求min是行不通的,只能先min后max。
下面引入"鞍点"概念,阐述什么情况下不等号能取等。
鞍点似乎多种定义,大概分为两大类,第一类所定义出的鞍点的意义包括着第二类定义出的。
第一种一般这样定义:
[1]当一个可微函数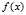 的驻点不是极值点时,该驻点也称为
的驻点不是极值点时,该驻点也称为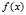 的一个鞍点。伍胜健,《数学分析(第三册)》
,北京大学出版社,p.96.
的一个鞍点。伍胜健,《数学分析(第三册)》
,北京大学出版社,p.96.
[2]A saddle point is a point in the domain of a function that is a stationary point but not a local extremum. Wikipedia page:Saddle point.
第二种一般这样定义:
若存在定义域内的点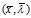 使得对定义域内的任意
使得对定义域内的任意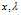 ,都有
,都有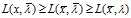 ,则称点
,则称点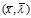 为函数
为函数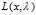 的一个鞍点。"鞍点定理在Lagrange乘数法上的应用",大学数学,Vol.25,
NO.2, Apr.2009.
的一个鞍点。"鞍点定理在Lagrange乘数法上的应用",大学数学,Vol.25,
NO.2, Apr.2009.
从下图中我们可以看出,原点显然满足鞍点的第一个定义,但是不满足鞍点的第二种定义,因为在两个坐标轴方向函数值都增加。由于问题的需要,在本文中我们采用第二种鞍点定义方法。这样做可能会使得一些函数得不到求解,如下图中的函数,但这类函数总可以通过坐标变换使得满足第二类鞍点定义。
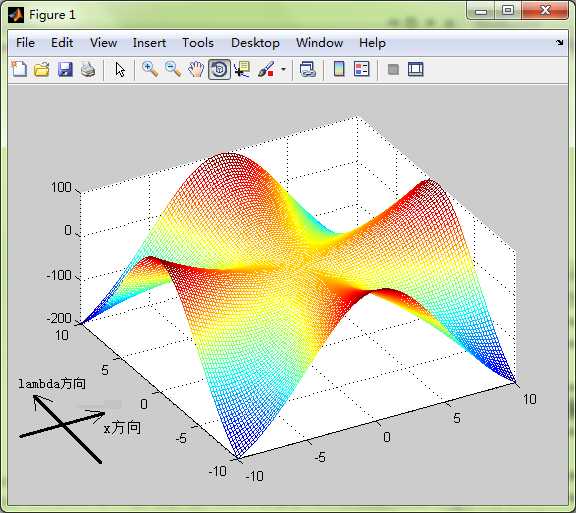
我们首先举出一个特例说明形如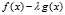 的
的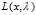 是有可能存在鞍点的。我们取
是有可能存在鞍点的。我们取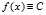 ,取
,取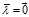 ,在集合
,在集合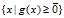 中任取一个作为
中任取一个作为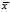 ,那么可以很容易的验证此
,那么可以很容易的验证此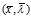 满足
满足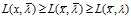 。
。
现在,我们假设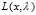 存在鞍点
存在鞍点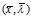 (此鞍点在定义域
(此鞍点在定义域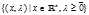 内),那么对任意的
内),那么对任意的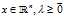 ,都有此关系
,都有此关系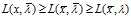 ,所以有:
,所以有:
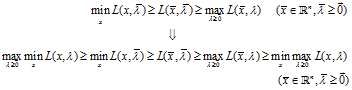
结合式可得:
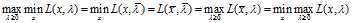
记问题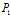 的最优解为
的最优解为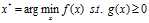 ,结合,并且由于
,结合,并且由于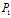 与
与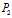 的等价性,我们立即可得
的等价性,我们立即可得
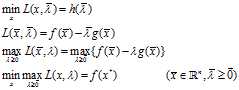
带入式得到:
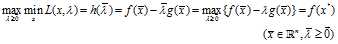
从第三个不等式我们可以得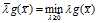 ,若
,若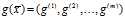 存在某个分量
存在某个分量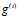 使得
使得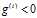 ,那么
,那么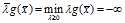 ,这说明在
,这说明在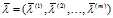 中至少存在一个分量
中至少存在一个分量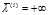 。这与
。这与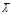 的存在性相矛盾。所以
的存在性相矛盾。所以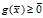 ,进一步可以得到
,进一步可以得到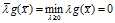 。于是,我们得到了这个称为"KKT最优化条件"的结果:
。于是,我们得到了这个称为"KKT最优化条件"的结果:
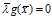
也正是因为这个条件,才使得许多算法拥有稀疏性,比如SVM。因为很多实际问题中向量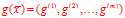 的大多数分量都不为零,这使得相对应于这些非零分量的
的大多数分量都不为零,这使得相对应于这些非零分量的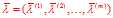 的分量必须为零,因此
的分量必须为零,因此 是稀疏的。
是稀疏的。
将式带入式可得:
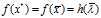
并且通过上一段的推导,我们还得到了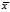 满足问题
满足问题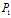 的约束条件
的约束条件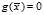 ,于是我们求得了问题
,于是我们求得了问题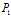 的一个最优解
的一个最优解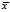 !
!
另外,今天了解到如何求鞍点已经有许多相当成熟的算法:直接法,预条件Krylov子空间法,MINRES算法,基于Uzawa类型的迭代方法,SOR算法,AOR算法。暂时只只知道他们的名字,还不知道它们长啥样。
现在我们还剩下两个问题: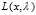 什么时候存在满足定义域限制
什么时候存在满足定义域限制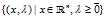 的鞍点
的鞍点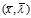 呢?如果
呢?如果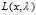 不存在鞍点,那又如何求解问题
不存在鞍点,那又如何求解问题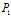 呢?
呢?
原文:http://www.cnblogs.com/mashiqi/p/3719101.html