背景
小K是个特么喜欢玩MC的孩纸。。。
描述
小K在MC里面建立很多很多的农场，总共n个，以至于他自己都忘记了每个农场中种植作物的具体数量了，他只记得
一些含糊的信息（共m个），以下列三种形式描述：农场a比农场b至少多种植了c个单位的作物，农场a比农场b至多
多种植了c个单位的作物，农场a与农场b种植的作物数一样多。但是，由于小K的记忆有些偏差，所以他想要知道存
不存在一种情况，使得农场的种植作物数量与他记忆中的所有信息吻合。
如果存在某种情况与小K的记忆吻合，输出”Yes”，否则输出”No”
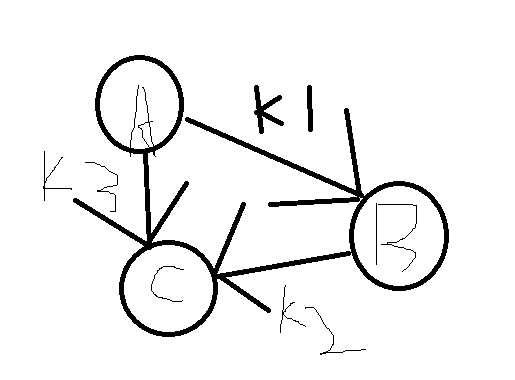那么注意到c - a <= k1 + k2,而c-a又 <= k3,所有我们求出k3和k1+k2之间的最小值即可，然后观察图，可以发现从a到c恰好有这样两条路径，而对应的最小值则是最短路，那么我们从减数向被减数连边，做最短路即可，但是本题只需要我们输出能不能行，也就是说每两个点之间能不能存在最短路，当一个有向图中出现了负环则不能形成最短路，因为在这个负环中每走一次则路径的长度更短，那么我们只需要判断一下图中是否有负环即可，那么可以用spfa判断，平时写的spfa算法都是bfs形式的，这次最好用dfs形式的，容易判断.#include <cstdio> #include <cstring> #include <iostream> #include <vector> #include <algorithm> using namespace std; const int maxn = 100010; struct node { int to, w; }; vector<node> e[maxn]; int vis[maxn],n,m,d[maxn]; bool flag; void add(int u, int v, int w) { node temp; temp.to = v; temp.w = w; e[u].push_back(temp); } void spfa(int x) { vis[x] = 1; for (int i = 0; i < e[x].size(); i++) { node v = e[x][i]; if (d[v.to] > d[x] + v.w) { if (vis[v.to]) //存在更短的路径又被访问过，说明存在负环 { flag = true; return; } d[v.to] = d[x] + v.w; spfa(v.to); } } vis[x] = false; return; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= m; i++) { int x,a,b,c; scanf("%d", &x); if (x == 1) { scanf("%d%d%d", &a, &b, &c); add(a, b, 0 - c); } if (x == 2) { scanf("%d%d%d", &a, &b, &c); add(b, a, c); } if (x == 3) { scanf("%d%d", &a, &b); add(a, b, 0); add(b, a, 0); } } flag = false; for (int i = 1; i <= n; i++) { d[i] = 0; spfa(i); if (flag) break; } if (flag) printf("No"); else printf("Yes"); return 0; }
原文：http://www.cnblogs.com/zbtrs/p/5811358.html