1、坐标点类
package cn.test.domain; public class Point { double x; double y; public Point(){ } public Point(double x, double y) { super(); this.x = x; this.y = y; } public double getX() { return x; } public void setX(double x) { this.x = x; } public double getY() { return y; } public void setY(double y) { this.y = y; } }
2、拟合类,带计算部分
package cn.test.normcdf; import java.io.IOException; import java.text.NumberFormat; import java.util.ArrayList; import java.util.Collections; import java.util.List; import javax.servlet.ServletException; import javax.servlet.http.HttpServlet; import javax.servlet.http.HttpServletRequest; import javax.servlet.http.HttpServletResponse; import net.sf.json.JSONArray; import net.sf.json.JSONObject; import org.apache.commons.math3.distribution.NormalDistribution; import cn.test.domain.Point; public class TestNormCdf extends HttpServlet { private ArrayList<Double> cyis = null; private ArrayList<Double> axis = null; public void doGet(HttpServletRequest request, HttpServletResponse response) throws ServletException, IOException { axis = new ArrayList<Double>(); cyis = new ArrayList<Double>(); // 初始化横坐标值 axis = initial(axis); /* axis = stand(axis); */ // 计算纵坐标值 //NormalDistribution normal = new NormalDistribution(); // 先排序 Collections.sort(axis); int n = axis.size(); /* for (int i = 0; i < axis.size(); i++) { cyis.add(normal.inverseCumulativeProbability((i + 1 - 0.5) / n)); }*/ for (int i = 0; i < axis.size(); i++) { cyis.add((i + 1 - 0.5) / n); } double sumX = getSum(axis); double sumY = getSum(cyis); double sumP2X = getPowSum(axis); double sumXY = getSumXY(axis, cyis); double a =(sumXY - (1 / axis.size()) * sumX * sumY) / (sumP2X - (1 /axis.size()) * sumX * sumX); double b = (1 / axis.size()) * (sumY - a*sumX); double pointx1 = axis.get(0); double pointx2 = axis.get(n - 1); double pointy1 = b+a * pointx1; double pointy2 = b+a * pointx2; //cyis = stand2(cyis); /*double x1 = axis.get((int) (n * 0.75)); double x2 = axis.get((int) (n * 0.25)); double y1 = cyis.get((int) (n * 0.75)); double y2 = cyis.get((int) (n * 0.25)); double dx = x1 - x2; double dy = y1 - y2; double a = dy / dx; double pointx1 = axis.get(0); double pointx2 = axis.get(n - 1); double centreX = 0.5 * (x1 + x2); double centreY = 0.5 * (y1 + y2); double pointy1 = centreY - a * (centreX - pointx1); double pointy2 = centreY + a * (pointx2 - centreX);*/ Double[][] array = new Double[axis.size() + 2][2]; NumberFormat ddf1 = NumberFormat.getNumberInstance(); ddf1.setMaximumFractionDigits(4); for (int i = 0; i < axis.size(); i++) { array[i][0] = Double.valueOf(ddf1.format(axis.get(i))); array[i][1] = Double.valueOf(ddf1.format(cyis.get(i))); } array[axis.size()][0] = Double.valueOf(ddf1.format(pointx1)); array[axis.size()][1] = Double.valueOf(ddf1.format(pointy1)); array[axis.size() + 1][0] = Double.valueOf(ddf1.format(pointx2)); array[axis.size() + 1][1] = Double.valueOf(ddf1.format(pointy2)); response.getWriter().write(JSONArray.fromObject(array).toString()); } public ArrayList<Double> stand2(ArrayList<Double> cyis) { int n = cyis.size(); NormalDistribution normal = new NormalDistribution(); for (int i = 0; i < cyis.size(); i++) { cyis.set(i, normal.cumulativeProbability(cyis.get(i))); } return cyis; } /* * public ArrayList<Double> stand(ArrayList<Double> list) { double average = * getAverage(list); double std = getStdVariance(list); for (int i = 0; i < * list.size(); i++) { list.set(i, (list.get(i) - average) / std); } return * list; } * * public double getStdVariance(ArrayList<Double> list) { double std = 0.0; * double average = getAverage(list); for (int i = 0; i < list.size(); i++) * { std += Math.pow((list.get(i) - average), 2); } return std / * list.size(); } * * public double getAverage(ArrayList<Double> list) { return getSum(list) / * list.size(); } */ public double getSum(ArrayList<Double> list) { double sum = 0.0; for (Double value : list) { sum += value; } return sum; } public double getSumXY(ArrayList<Double> X, ArrayList<Double> Y) { double sum = 0.0; for (int i = 0; i < X.size(); i++) { sum += X.get(i) * Y.get(i); } return sum; } public double getPowSum(ArrayList<Double> list) { double sum = 0.0; for (Double value : list) { sum += Math.pow(value, 2); } return sum; } public ArrayList<Double> initial(ArrayList<Double> axis) { axis = new ArrayList<Double>(); axis.add(9.0); axis.add(11.0); axis.add(15.0); axis.add(20.0); axis.add(30.0); axis.add(40.0); axis.add(35.0); axis.add(80.0); axis.add(50.0); axis.add(60.0); axis.add(55.0); axis.add(45.0); axis.add(65.0); axis.add(70.0); axis.add(58.0); axis.add(72.0); axis.add(66.0); axis.add(59.0); return axis; } public void doPost(HttpServletRequest request, HttpServletResponse response) throws ServletException, IOException { doGet(request, response); } }
3、html部分代码
<script src="http://cdn.hcharts.cn/jquery/jquery-1.8.3.min.js"></script> <script src="${pageContext.request.contextPath}/js/highcharts.js" ></script> <script type="text/javascript"> $(function(){ $.post("/Test_Polyfit/TestNormCdf",null,function(data){ var array=eval(data); $("#container").highcharts({ chart:{ zoomType:‘xy‘ }, title:{ text:‘Normal Probability of Wait Time‘ }, xAxis:{ title:{ enabled:true, text:‘Wait Time‘ }, startOnTick: true, endOnTick: true, showLastLabel: true }, yAxis:{ title:{ text:‘Probability in normal distribution‘ }, min:0, max:1, staggerLines:20, allowDecimals:true }, legend:{ layout:‘vertical‘, align:‘left‘, verticalAlign: ‘top‘, x: 100, y: 70, floating: true, backgroundColor: ‘#FFFFFF‘, borderWidth: 1 }, plotOptions: { scatter: { marker: { radius: 5, states: { hover: { enabled: true, lineColor: ‘rgb(100,100,100)‘ } } }, states: { hover: { marker: { enabled: false } } }, tooltip: { headerFormat: ‘<b>{series.name}</b><br>‘, pointFormat: ‘{point.x} cm, {point.y} kg‘ } } }, series: [{ type:‘scatter‘, name: ‘point‘, color: ‘rgba(223, 83, 83, .5)‘, data: array },{ type:‘line‘, name: ‘polyfitline‘, color: ‘black‘, data: [array.pop(),array.pop()] }] }); }); }); </script> </head> <body> <div id="container"></div>
4、最后实现的效果
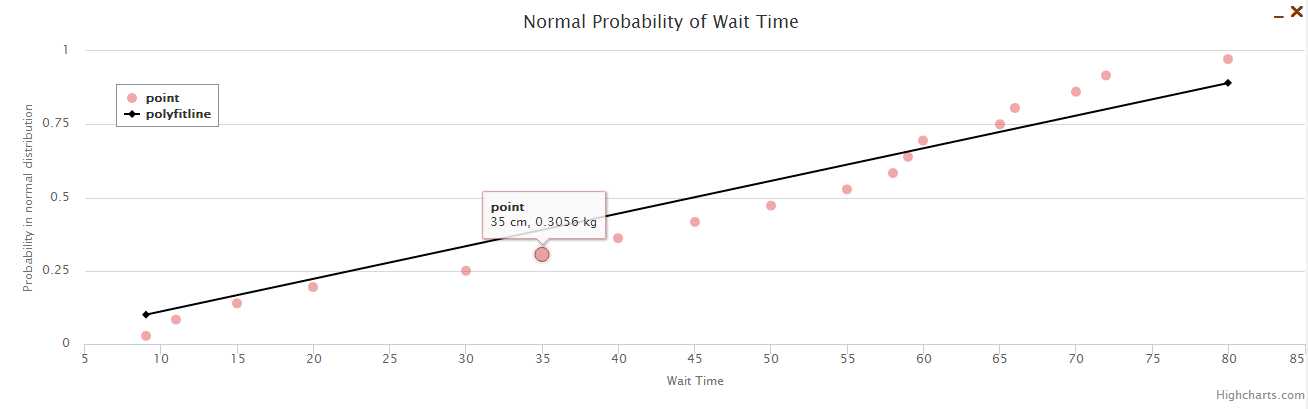
6、基于highcharts实现的线性拟合,计算部分在java中实现,画的是正态概率图
原文:http://www.cnblogs.com/weizhen/p/5823877.html