继续以上一期的样本为例,雌性老鼠和雄性老鼠,在注射毒素后,经过一段时间,观察老鼠死亡和存活情况。
研究的问题是:老鼠在注射毒液后,死亡和存活情况,会不会跟性别有关?
样本数据如下所示: (a代表雄性老鼠 b代表雌性老鼠 0代表死亡 1 代表活着 tim 代表注射毒液后,经过多长时间,观察结果)
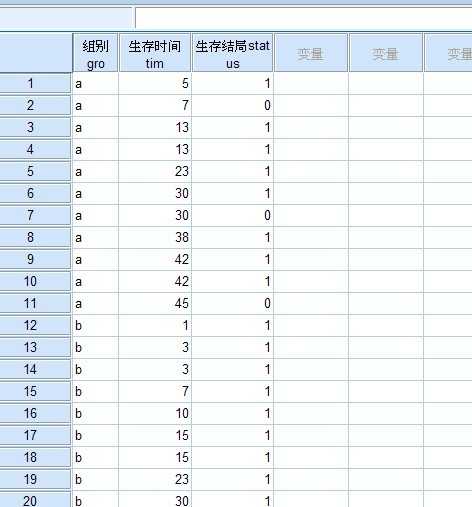
点击“分析”——比较均值———单因素AVOVA, 如下所示:
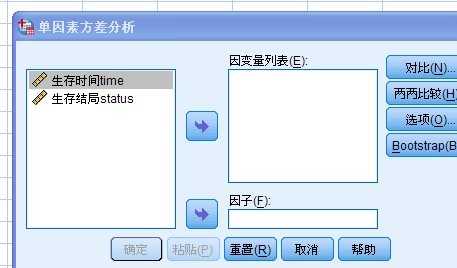
从上图可以看出,只有“两个变量”可选, 对于“组别(性别)”变量不可选, 这里可能需要进行“转换”对数据重新进行编码,
点击“转换”—“重新编码为不同变量” 将a,b"分别用8,9进行替换,得到如下结果”
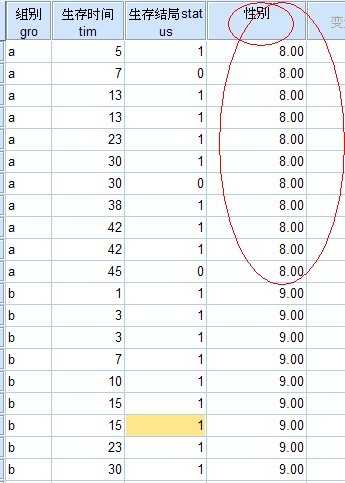
此时的8 代表a(雄性老鼠) 9代表b雌性老鼠, 我们将“生存结局”变量移入“因变量列表”框内, 将“性别”移入“因子”框内,点击“两两比较”按钮,如下所示:
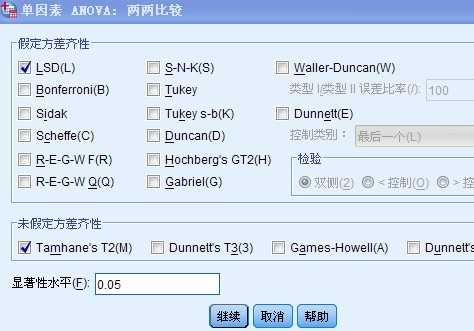
“ 勾选“将定方差齐性”下面的 LSD 选项, 和“未假定方差齐性”下面的Tamhane‘s T2选项 点击继续
点击“选项”按钮,如下所示:
勾选“描述性”和“方差同质检验” 以及均值图等选项,得到如下结果:
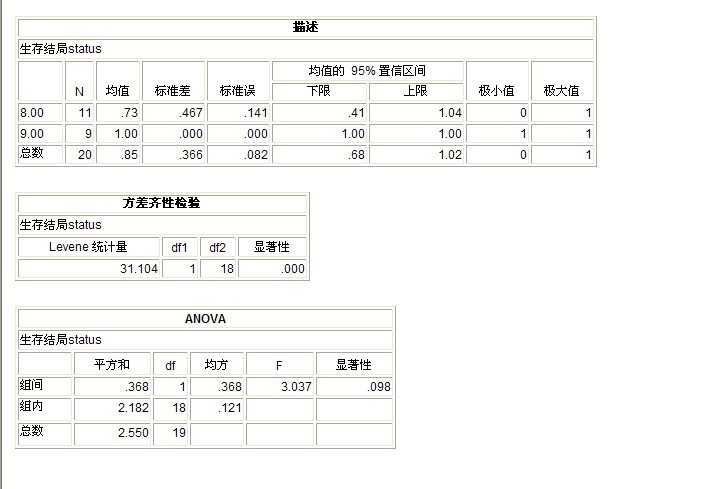
结果分析:方差齐性检验结果, “显著性”为0, 由于显著性0<0.05 所以,方差齐性不相等, 在一般情况下,不能够进行方差分析
但是对于SPSS来说,即使方差齐性不相等,还是可以进行方差分析的,
由于此样本组少于三组,不能够进行多重样本对比
从结果来看“单因素 ANOVA” 分析结果,显著性0.098,由于0.098>0.05 所以可以得出结论:
生存结局受性别的影响不显著
很多人,对这个结果可能存在疑虑,下面我们来进一步进行论证,由于“方差齐性不相等”下面我们来进行“非参数检验”检验结果如下所示: (此处采用的是“Kruskal-Wallis "检验方法)

通过“Kruskal-Wallis ”检验方法,我们得出“sig=0.098" 跟我们先前分析的结果一样, 都是0.098, 事实得到论证。
原文地址:http://hi.baidu.com/shuaibing001/item/192579d8e7e3fdfecb0c39ba
SPSS-单因素方差分析(ANOVA) 案例解析,布布扣,bubuko.com
原文:http://www.cnblogs.com/qiernonstop/p/3720401.html