点积、向量夹角:
无论对于空间向量还是平面向量,我们所熟知的是:给出任意两个向量,我们都能够根据公式计算它们的夹角,但是这个夹角必须是将两个向量的起点重合后所夹成的小于等于π的角,可是,这是为什么呢?
它其实来源于如下的定理(这里的定理和证明过程以三维向量为例,对于二维向量,可做完全一致的推导):
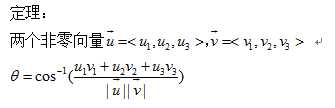
证明:
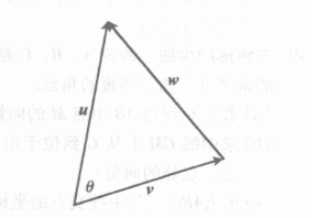
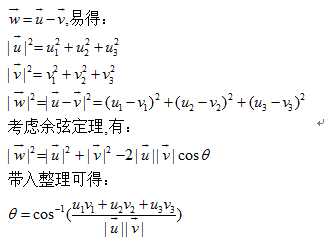
考虑在如下的一个三角形中。
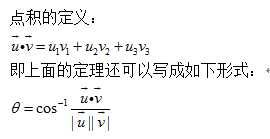
通过这个定理的证明过程就能够理解:为什么我们求向量夹角用点积;两个向量之间的点积为什么等于两个向量模长再乘以夹角的余弦值;为什么我们求出来的角是起点重合的两个向量夹出小于π的角(因为我们基于一个三角形,两向量起点重合是的向量w能够按照上文中给出的形式计算)。
《University Calculus》-chape10-向量与空间几何学-向量夹角
原文:http://www.cnblogs.com/rhythmic/p/5850737.html