题目:
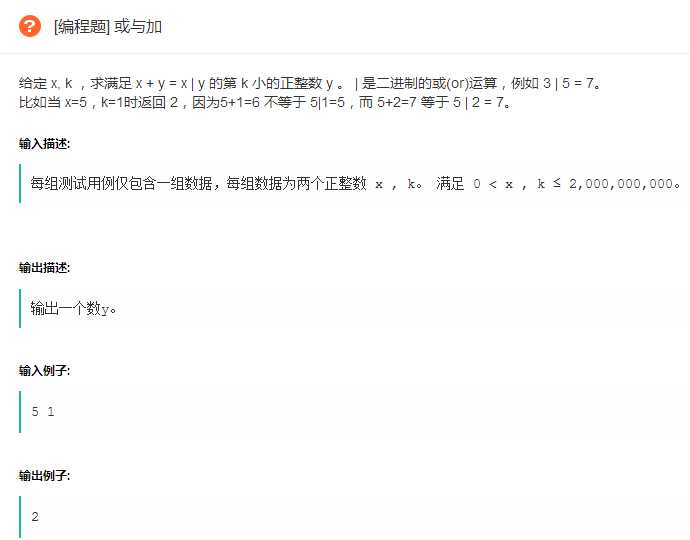
这个题做到最后,时间不是很够,题目内容比较简单,求出第k个正整数符合x+y=x|y,然而这个k的取值范围非常大(k<=2000000000),所以可以不用考虑穷举法,当然,时间不够的话写个穷举试试运气也可以。
穷举法:
1 import java.util.Scanner; 2 3 /** 4 * Created by Administrator on 2016/9/6. 5 */ 6 7 public class Main { 8 public static void main(String[] args) { 9 Scanner scanner = new Scanner(System.in); 10 int x = scanner.nextInt(); 11 int k = scanner.nextInt(); 12 int n = 0; 13 int result = 0; 14 for (int i = 1; i <= 2000000000; i++) { 15 if ((x + i) == (x | i)) { 16 n += 1; 17 } 18 if (n == k) { 19 result = i; 20 break; 21 } 22 } 23 System.out.println(result); 24 } 25 }
这里提交会提示超时,所以这个算法是不行的,比较循环的次数太多。
第一个想法是能不能减少循环次数,但是考虑到要求第k个,也就是不能省略掉其中一些否则会遗漏,所以只能考虑能否不使用循环求得。
因为这里用到了位运算,所以可以通过二进制来演算一下。
假设数据x=5,k=1的时候,y=2,分别用二进制进行表示:
5D = 0101B
2D = 0010B
7D = 0111B
这里其实已经可以发现规律了。
x+y是把x和y每一个二进制位进行相加,1+1就进位
x|y则是每个二进制位置对应的进行或运算(有1得1)
这个题目中,x的值是固定的,也就是x的二进制数中1的位置和数目是固定的,所以进行或运算的时候,结果中对应的位上都应该是1。
现在考虑相加的情况,假设y与x中某一对应的位置都是1,就需要进行进位,也就是这个位置会变成0,显然x+y!=x|y。
考虑x中0的影响,因为在相加或者或运算的时候,0都不会影响到运算结果,所以结论很显然:
yB的对应于xB上所有为1的位均为0,则必有x+y=x|y。
现在考虑如何得到第k个。
因为有上面的规律,我们可以得知,y中为1的位只能对应于x中为0的位。
这里就很简单了,我们只需要求出k的二进制值,并且把这个二进制的值从低位逐个填入x为0的位即可得到相加的结果。
如:5+2=5|2=7 k=1
5D = 0101B
1D = 0001B
我们把1的二进制填入至x的二进制为0的地方则能得到0111B,也就是十进制的7。7-5=2,就能得到y的值。
再举一个例子:x=5, k=2
5D = 0101B
2D = 0010B
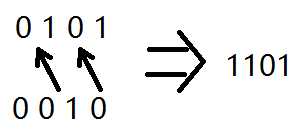
把2的二进制从低位开始填入5的二进制数中为0的地方,即可得到1101B,也就是13,所以y=13-5=8。
实际上,我们只需要把x中对应为1的地方改为1,就能直接得到y的值,相当于减去x。
所以我们在实际构造的时候,可以这样做:
逆序遍历x的每一位
如果为1,则往结果的头部填充一个0(减法)
否则将k中的最后一位填入结果的头部,并退出k的最后一位,此时如果k已经为空,则退出遍历。
判断x是否已经遍历完,如果是,将k剩余的位一次填充到结果的头部。
AC代码:
1 import java.util.Scanner; 2 3 /** 4 * Created by Administrator on 2016/9/6. 5 */ 6 7 public class Main { 8 public static void main(String[] args) { 9 Scanner scanner = new Scanner(System.in); 10 int x = scanner.nextInt(); 11 int k = scanner.nextInt(); 12 String x_str = Integer.toBinaryString(x); 13 String k_str = Integer.toBinaryString(k); 14 StringBuilder sb = new StringBuilder(); 15 int pointer = k_str.length() - 1; 16 for (int i = x_str.length() - 1; i >= 0; i--) { 17 if (x_str.charAt(i) == ‘1‘) { 18 sb.insert(0, "0"); 19 } else { 20 sb.insert(0, k_str.charAt(pointer)); 21 pointer -= 1; 22 if (pointer < 0) { 23 break; 24 } 25 } 26 if (i == 0 && pointer >= 0) { 27 sb.insert(0, k_str.substring(0, pointer + 1)); 28 } 29 } 30 System.out.println(Long.parseLong(sb.toString(), 2)); // 使用Long是因为结果可能会超过Integer的表示范围 31 } 32 }
算法面试题-今日头条2017客户端工程师实习生笔试题4:或与加
原文:http://www.cnblogs.com/Fndroid/p/5855810.html