题目描述
某国法律规定,只要一个由N*M个小方块组成的旗帜符合如下规则,就是合法的国旗。(毛熊:阿嚏——)
-
从最上方若干行(>=1)的格子全部是白色的。
-
接下来若干行(>=1)的格子全部是蓝色的
- 剩下的行(>=1)全部是红色的
现有一个棋盘状的破布,分成了N行M列的格子,每个格子是白色蓝色红色之一,小a希望把这个布改成该国国旗,方法是在一些格子上涂颜料,盖住之前的颜色。
小a很懒,希望涂最少的格子,使这块破布成为一个合法的国旗。
输入输出格式
输入格式:
第一行是两个整数,N,M
接下来N行是一个矩阵,矩阵的每一个小方块是‘W‘(白),‘B‘(蓝),‘R‘(红)中的一个
输出格式:
一个整数,表示至少需要涂多少块。
输入输出样例
4 5 WRWRW BWRWB WRWRW RWBWR
11
说明
样例解释:
目标状态是
WWWWW
BBBBB
RRRRR
RRRRR一共需要改11个格子
对于100%的数据,N,M<=50
100分代码:
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int N=55; char mp[N][N],bf[N][N],w[N],b[N],r[N]; int n,m,ans=0x7fffffff; inline int check(char *a,char *b){ int res=0; for(int i=1;i<=m;i++) if(a[i]!=b[i]) res++; return res; } void dfs(){ memcpy(bf,mp,sizeof mp); for(int i=1;i<=n-2;i++){ int tans=0; for(int q=1;q<=i;q++){ tans+=check(mp[q],w); memcpy(mp[q],w,sizeof w); } for(int j=i+1;j<=n-1;j++){ int t2=0,t3=0; for(int q=i+1;q<=j;q++){ t2+=check(mp[q],b); memcpy(mp[q],b,sizeof b); } for(int q=j+1;q<=n;q++){ t3+=check(mp[q],r); memcpy(mp[q],r,sizeof r); } tans+=t2+t3; ans=min(ans,tans); for(int q=i+1;q<=n;q++) memcpy(mp[q],bf[q],sizeof bf[q]); tans-=t2+t3; } for(int q=1;q<=n;q++) memcpy(mp[q],bf[q],sizeof bf[q]); } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%s",mp[i]+1); for(int i=1;i<=m;i++) w[i]=‘W‘; for(int i=1;i<=m;i++) b[i]=‘B‘; for(int i=1;i<=m;i++) r[i]=‘R‘; dfs(); printf("%d\n",ans); return 0; }
题目描述
小a住的国家被僵尸侵略了!小a打算逃离到该国唯一的国际空港逃出这个国家。
该国有N个城市,城市之间有道路相连。一共有M条双向道路。保证没有自环和重边。
K个城市已经被僵尸控制了,如果贸然闯入就会被感染TAT...所以不能进入。由其中任意城市经过不超过S条道路就可以到达的别的城市,就是危险城市。换句话说只要某个没有被占城市到某个被占城市不超过s距离,就是危险。
小a住在1号城市,国际空港在N号城市,这两座城市没有被侵略。小a走每一段道路(从一个城市直接到达另外一个城市)得花一整个白天,所以晚上要住旅店。安全的的城市旅馆比较便宜要P元,而被危险的城市,旅馆要进行安保措施,所以会变贵,为Q元。所有危险的城市的住宿价格一样,安全的城市也是。在1号城市和N城市,不需要住店。
小a比较抠门,所以他希望知道从1号城市到N号城市所需要的最小花费。
输入数据保证存在路径,可以成功逃离。输入数据保证他可以逃离成功。
输入输出格式
输入格式:
第一行4个整数(N,M,K,S)
第二行2个整数(P,Q)
接下来K行,ci,表示僵尸侵占的城市
接下来M行,ai,bi,表示一条无向边
输出格式:
一个整数表示最低花费
输入输出样例
13 21 1 1 1000 6000 7 1 2 3 7 2 4 5 8 8 9 2 5 3 4 4 7 9 10 10 11 5 9 7 12 3 6 4 5 1 3 11 12 6 7 8 11 6 13 7 8 12 13
11000
说明
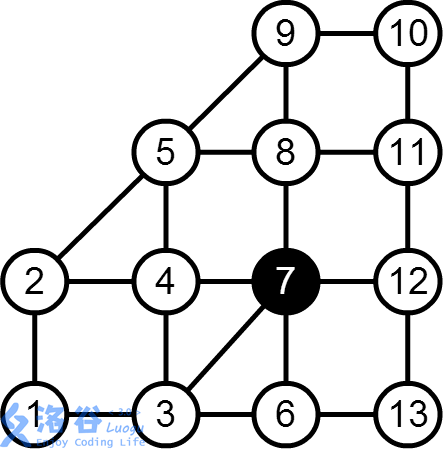
对于20%数据,N<=50
对于100%数据,2 ≦ N ≦ 100000, 1 ≦ M ≦ 200000, 0 ≦ K ≦ N - 2, 0 ≦ S ≦ 100000
1 ≦ P < Q ≦ 100000
100分代码:
#include<cstdio> #include<cstring> #include<queue> using namespace std; inline const int read(){ register int x=0,f=1; register char ch=getchar(); while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } #define ll long long #define xx first #define yy second #define pir pair<int,int> const int N=2e5+10; struct node{ int v,next; }e[N<<1]; int tot,head[N],js[N],pw[N]; bool vis[N],JS[N]; int n,m,s,k,P,Q; void add(int x,int y){ e[++tot].v=y; e[tot].next=head[x]; head[x]=tot; } void bfs(int S,int lim){ int dis[N]={0}; memset(vis,0,sizeof vis); queue<pir>q; q.push(make_pair(S,0)); vis[S]=1; while(!q.empty()){ pir h=q.front();q.pop(); if(h.yy==lim) continue; for(int i=head[h.xx];i;i=e[i].next){ if(!dis[e[i].v]){ dis[e[i].v]=dis[h.xx]+1; if(!vis[e[i].v]){ vis[e[i].v]=1; pw[e[i].v]=Q; q.push(make_pair(e[i].v,dis[e[i].v])); } } } } } void spfa(){ ll dis[N]; memset(dis,127,sizeof dis); memset(vis,0,sizeof vis); queue<int>q; q.push(1); dis[1]=0; vis[1]=1; while(!q.empty()){ int h=q.front();q.pop(); vis[h]=0; for(int i=head[h];i;i=e[i].next){ int v=e[i].v; if(JS[v]) continue; if(dis[v]>dis[h]+(ll)pw[v]){ dis[v]=dis[h]+(ll)pw[v]; if(!vis[v]){ vis[v]=1; q.push(v); } } } } printf("%lld\n",dis[n]); } int main(){ n=read(),m=read(),k=read(),s=read(); P=read(),Q=read(); for(int i=1;i<=k;i++) js[i]=read(); for(int i=1,x,y;i<=m;i++) x=read(),y=read(),add(x,y),add(y,x); for(int i=1;i<=k;i++) bfs(js[i],s); for(int i=1;i<=n;i++) if(!pw[i]) pw[i]=P;pw[n]=0; for(int i=1;i<=k;i++) JS[js[i]]=1; spfa(); return 0; }
题目描述
一个机器人从xoy平面出发,按照给定的程序运行,程序中的一个字母E\S\W\N分别表示机器人往东\南\西\北走1米。我们会给出则一段有N个指令的程序。机器人将连续的执行这段程序K次。从原点开始,机器人每执行完一步,就会在地上做一个标记(原点也留了一个)。现在问,所有程序结束后,有多少个1*1的小方形,其四个顶点都被坐上了标记?
输入输出格式
输入格式:
第一行两个整数,N,K
第一行是长度为N的字符串,每个字符只会是一个字母E\S\W\N分别表示机器人往东\南\西\北走1米。
输出格式:
一个整数,表示符合要求的小方格数量
输入输出样例
6 3 SEENWS
6
说明
20% N<=50,K=1;
另外20% k=1
另外20% N<=50
100% N<=100000,0<k<=10^9
80分代码:
#include<cstdio> #include<cstring> #include<algorithm> #define ll long long using namespace std; const int N=1e5+100; struct node{ int x,y; bool operator < (const node a) const { if(x==a.x) return y<a.y; return x<a.x; } bool operator == (const node a) const{ return x==a.x&&y==a.y; } bool operator != (const node a) const{ return x!=a.x||y!=a.y; } }ans[N<<4]; char s[N]; int cnt,res,n,k; bool vis[3010][3010]; node deal(int sx,int sy){ ans[++cnt]=(node){sx,sy}; int len=strlen(s); for(int i=0;i<len;i++){ if(s[i]==‘N‘) ans[++cnt]=(node){++sx,sy}; else if(s[i]==‘S‘) ans[++cnt]=(node){--sx,sy}; else if(s[i]==‘W‘) ans[++cnt]=(node){sx,--sy}; else if(s[i]==‘E‘) ans[++cnt]=(node){sx,++sy}; } node t; t.x=sx; t.y=sy; return t; } int ef(node x){ int l=1,r=cnt; while(l<r){ int mid=l+r>>1; if(x<ans[mid]||ans[mid]==x) r=mid; else l=mid+1; } return l; } int solve(){ sort(ans+1,ans+cnt+1); cnt=unique(ans+1,ans+cnt+1)-(ans+1); for(int i=1;i<=cnt;i++){ if(!vis[ans[i].x+1500][ans[i].y+1500]){ node la=(node){ans[i].x,ans[i].y+1}; node ra=(node){ans[i].x-1,ans[i].y}; node aa=(node){ans[i].x-1,ans[i].y+1}; int lp=ef(la); if(ans[lp]!=la) continue; int rp=ef(ra); if(ans[rp]!=ra) continue; int pp=ef(aa); if(ans[pp]!=aa) continue; res++; vis[ans[i].x+1500][ans[i].y+1500]=1; } } } int main(){ scanf("%d%d%s",&n,&k,s); node t=deal(0,0); solve(); int r1=res; if(k==1){printf("%d",res);return 0;} else{ deal(t.x,t.y); solve(); int r2=res-r1; printf("%lld\n",(ll)r1+(ll)r2*(ll)(k-1)); //cout<<(ll)r1+(ll)r2*(ll)(k-1); } return 0; }