解决思路:将输入字符串1看作行, 输入字符串2看作列,构成二位数组,然后将对角线匹配字符的值标记为1,计算满足条件的匹配字符个数即可。
基本思想: 空间换时间,动态规划。
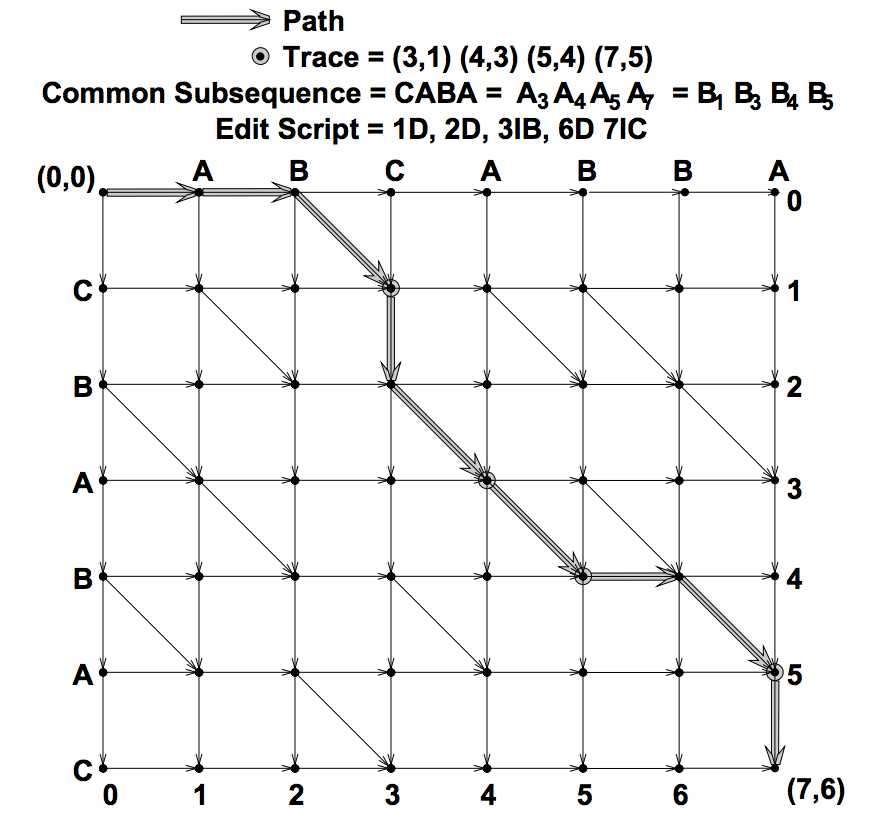
图解与公式(只针对最长子序列,最长子串类似)
状态转移方程
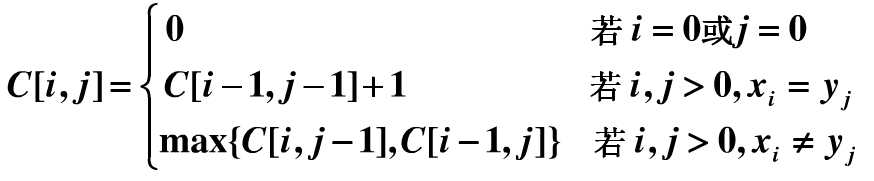
直观版:
最长子序列
1 /** 2 * find longest common sequence from two input string 3 * @param s1 4 * @param s2 5 * @return length of longest common sequence 6 */ 7 public static int LCS(String s1, String s2) { 8 int[][] c = new int[s1.length()][s2.length()]; 9 10 // initialize the elements without top left element 11 for(int i=0; i<s1.length();i++){ 12 if (s1.charAt(i) == s2.charAt(0)) { 13 c[i][0] = 1; 14 } 15 } 16 for(int j = 0; j<s2.length();j++){ 17 if (s1.charAt(0) == s2.charAt(j)) { 18 c[0][j] = 1; 19 } 20 } 21 for (int i = 1; i < s1.length(); i++) { 22 for (int j = 1; j < s2.length(); j++) { 23 if (s1.charAt(i) == s2.charAt(j)) { 24 c[i][j] = c[i - 1][j - 1] + 1; 25 } else if (c[i][j - 1] > c[i - 1][j]) { 26 c[i][j] = c[i][j - 1]; 27 } else { 28 c[i][j] = c[i - 1][j]; 29 } 30 } 31 } 32 return c[s1.length() - 1][s2.length() - 1]; 33 }
最长子序列也可以用稳定的排序算法先排序,再匹配。如采用归并排序算法(注意,快速排序不稳定)。
最长子串
1 /** 2 * find longest substring from two input string 3 * 4 * @param s1 5 * @param s2 6 * @return length of longest substring 7 */ 8 public static int LSS(String s1, String s2) { 9 int[][] c = new int[s1.length()][s2.length()]; 10 int max = 0; 11 12 // initialize the elements without top left element 13 for(int i=0; i<s1.length();i++){ 14 if (s1.charAt(i) == s2.charAt(0)) { 15 c[i][0] = 1; 16 } 17 } 18 for(int j = 0; j<s2.length();j++){ 19 if (s1.charAt(0) == s2.charAt(j)) { 20 c[0][j] = 1; 21 } 22 } 23 24 for (int i = 1; i < s1.length(); i++) { 25 for (int j = 1; j < s2.length(); j++) { 26 if (s1.charAt(i) == s2.charAt(j)) { 27 c[i][j] = c[i - 1][j - 1] + 1; 28 if (c[i][j] > max) { 29 max = c[i][j]; 30 } 31 } 32 } 33 } 34 return max; 35 }
优化版:
待续..
优化基本思想:
可以采用递归方式,尽早舍弃不符合要求的匹配。
对于优化最长子串,
可以优先查找最长子串,如果发现一个匹配,就一直找下去,同时将最终的不匹配标记为-1而不是0.
如果剩余的可能匹配长度小于已找到的长度,则停止递归操作,直接return.
其他相关算法
Horspool‘s Algorithm and Boyer-Moore Algorithm
原文:http://www.cnblogs.com/7explore-share/p/5927292.html