链接:http://www.zhihu.com/question/29885222/answer/100043031
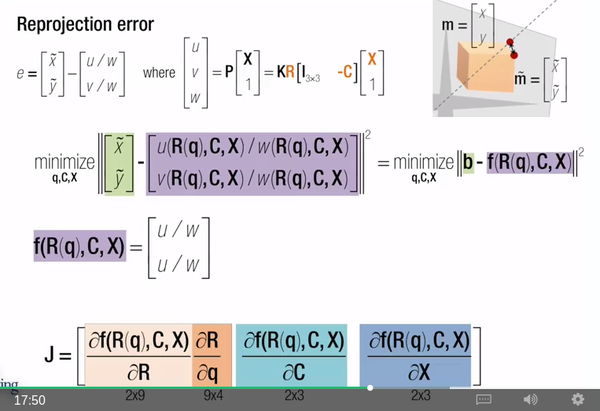
首先一切建立在相机模型 x = kPX 上
x,X分别代表图片和空间中的二维三维齐次坐标,
k为相机内参矩阵,
P = [R | t] 为空间坐标系到相机坐标系的 orientation- R 和 transformation- t
1, 首先对某一场景多角度多位置得到很多初始数据,选择其中的某两个来初始化,选定其中一个为空间原点。

2. 通过SIFT ,SURF等特征点查找匹配之后,用 8点法 和 RANSAC,多次计算两张图之间的Fundamental Matrix,选择其中最好的一个。

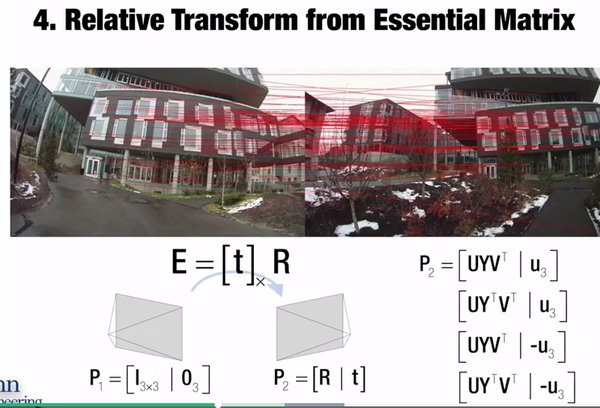
3. 用F-matrix 计算 Essential-matrix

4, 用 E-matrix 计算相机的 R 和 T,需要用SVD分解,因为orientation R是一个正交阵。
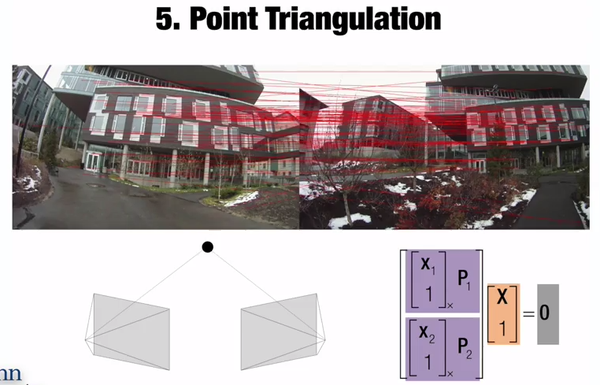
5, 得到两个相机之间的P矩阵之后,通过对应点,用 Triangulation 计算对应点的空间坐标。
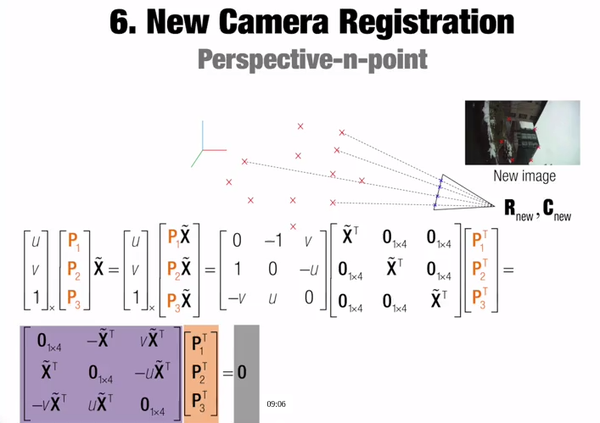
6. 第三个位置的照片,直接根据已有的上步计算的点,与第三个位置图片上点的对应关系,计算P矩阵。
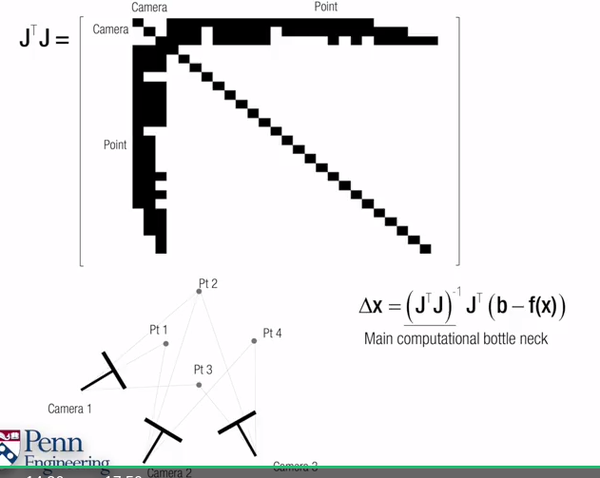
7. 最后全局优化,Bundle Adjustment
8, Bundle Adjustment所有的艺术就是优化 hessian matrix的逆矩阵。
------------------------------------------------------------------------------------------------------------
推荐宾大Shi Jianbo教授在Coursera上的公开课 Robotics:Perception
上面所有的截图都来自他最后一次课的视频讲义截图
https://www.coursera.org/learn/robotics-perception/home/welcome
配合视觉圣经 Multiple View Geometry来看简直完美。Ransac, Bundle-adjustment, 2-View, Homography全部都有。一共四周,有线性代数基础(主要是SVD用来解线性方程),作业用Matlab.
第一周作业: Dolly Zoom
第二周作业: 平面摄影几何,广告牌在视频中的投影,类似2D增强现实
第三周作业: 在平面Barcode上通过sift检测特征点,通过H矩阵计算相机位置,做3D增强现实
第四周作业: 3D重建
[SLAM] 02 Some algorithms of 3D reconstruction
原文:http://www.cnblogs.com/jesse123/p/5869835.html