定义:AVL树是每个节点左子树和右子树的高度差最大为1的二叉查找树
不平衡节点:假设在懒惰删除(删除操作时,并不删除节点,只是对节点进行特定标记)的条件下,插入操作有可能破坏AVL树的平衡特性。
如果插入节点导致平衡性被破坏,那么平衡性遭到破坏的节点只可能出现在插入节点到根节点的路径上。因为插入操作只会改变
插入节点的父节点的高度,而这些父节点就再这条路径上。
调整:对于平衡性遭到破坏的节点,需要对其进行调整以恢复平衡性。调整的方法称为旋转,针对不同的插入情况,调整操作稍有不同。
下面先对插入情况进行分类。假设插入节点后,平衡性遭到破坏的节点为A:
1、插入节点是A节点的左儿子的左儿子(左外部)
2、插入节点是A节点的左儿子的右儿子(左内部)
3、插入节点是A节点的右儿子的右儿子(右外部)
4、插入节点是A节点的右儿子的左儿子(右内存)
其中,左外部和右外部相似的,通过单旋转来调整平衡性;左内部和右内部是相似的,通过双旋转来调整平衡性。
单旋转:
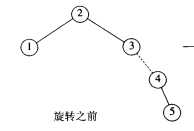
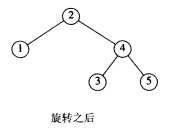
上图中,插入的节点5,属于右外部的情况,节点3平衡性遭到破坏,所以对节点3进行旋转。
把节点3绕着它的右儿子节点4旋转,直到成为节点4的左儿子。由于二叉树的性质,节点3比节点4小,
所以作为节点4的左儿子没有问题。如果节点4本来存在左儿子,那么把它拆下来接到节点3,成为节点
3的右儿子。节点3经过旋转已经没有右儿子,所以这种操作没有问题。最后用节点4代替原来的节点3,
至此,单旋转操作完成。
对于左外部的情况类似。
双旋转:
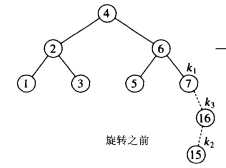
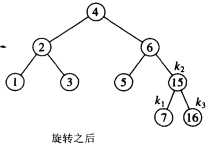
上图中,插入节点15,属于右内部情况。节点k1的平衡性遭到破坏,先对节点k1的右儿子k3做一次
左外部的单选转,然后再对节点k1做一次右外部的单选转,就完成了单旋转操作。
通过观察知道,无论是单旋转还是双旋转,平衡性遭到破坏时,需要对三个节点的位置进行调整。我们需要做的是,
调整三个节点的位置,使它们符合二叉树的排序特性(任一节点大于左儿子,小于右儿子),如果它们原来有左右儿子,
只需要把它们的左右儿子重新放到合适的位置就可以了。而旋转只是实现的方法,因为根据二叉树的排序特性,我们知道
这三个节点的大小关系而不用重新比较大小,只需通过旋转就可以了。
原文:http://www.cnblogs.com/jc-nogame/p/5918322.html