| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 11215 | Accepted: 5575 |
Description
The roads themselves are also rather interesting. Due to the strange customs of the island, the roads are arranged so that they never meet at intersections, but rather pass over or under each other using bridges and tunnels. In this way, each road runs between two specific tourist attractions, so that the tourists do not become irreparably lost.
Unfortunately, given the nature of the repairs and upgrades needed on each road, when the construction company works on a particular road, it is unusable in either direction. This could cause a problem if it becomes impossible to travel between two tourist attractions, even if the construction company works on only one road at any particular time.
So, the Road Department of Remote Island has decided to call upon your consulting services to help remedy this problem. It has been decided that new roads will have to be built between the various attractions in such a way that in the final configuration, if any one road is undergoing construction, it would still be possible to travel between any two tourist attractions using the remaining roads. Your task is to find the minimum number of new roads necessary.
Input
Output
Sample Input
Sample Input 1 10 12 1 2 1 3 1 4 2 5 2 6 5 6 3 7 3 8 7 8 4 9 4 10 9 10 Sample Input 2 3 3 1 2 2 3 1 3
Sample Output
Output for Sample Input 1 2 Output for Sample Input 2 0
Source
大致题意:
某个企业想把一个热带天堂岛变成旅游胜地,岛上有N个旅游景点,任意2个旅游景点之间有路径连通(注意不一定是直接连通)。而为了给游客提供更方便的服务,该企业要求道路部门在某些道路增加一些设施。
道路部门每次只会选择一条道路施工,在该条道路施工完毕前,其他道路依然可以通行。然而有道路部门正在施工的道路,在施工完毕前是禁止游客通行的。这就导致了在施工期间游客可能无法到达一些景点。
为了在施工期间所有旅游景点依然能够正常对游客开放,该企业决定搭建一些临时桥梁,使得不管道路部门选在哪条路进行施工,游客都能够到达所有旅游景点。给出当下允许通行的R条道路,问该企业至少再搭建几条临时桥梁,才能使得游客无视道路部门的存在到达所有旅游景点?
解题思路:
同题:poj3177 http://www.cnblogs.com/shenben/p/5839786.html
首先建立模型:
给定一个连通的无向图G,至少要添加几条边,才能使其变为双连通图。
模型很简单,正在施工的道路我们可以认为那条边被删除了。那么一个图G能够在删除任意一条边后,仍然是连通的,当且仅当图G至少为双连通的。
显然,当图G存在桥(割边)的时候,它必定不是双连通的。桥的两个端点必定分别属于图G的两个【边双连通分量】(注意不是点双连通分量),一旦删除了桥,这两个【边双连通分量】必定断开,图G就不连通了。但是如果在两个【边双连通分量】之间再添加一条边,桥就不再是桥了,这两个【边双连通分量】之间也就是双连通了。
那么如果图G有多个【边双连通分量】呢?至少应该添加多少条边,才能使得任意两个【边双连通分量】之间都是双连通(也就是图G是双连通的)?
这个问题就是本题的问题。要解决这个问题:
1、 首先要找出图G的所有【边双连通分量】。
Tarjan算法用来寻找图G的所有【边双连通分量】是最简单有效的方法,因为Tarjan算法在DFS过程中会对图G所有的结点都生成一个Low值,而由于题目已表明任意两个结点之间不会出现重边,因此Low值相同的两个结点必定在同一个【边双连通分量】中! (如果是有重边的话,那么不同的low值是可能是属于同一个边双连通分量的,这个时候就要通过其他方法去求解边双连通分量。不过这不是本题要讨论的)
2、 把每一个【边双连通分量】都看做一个点(即【缩点】)
也有人称【缩点】为【块】,都是一样的。其实缩点不是真的缩点,只要利用Low值对图G的点分类处理,就已经缩点了。
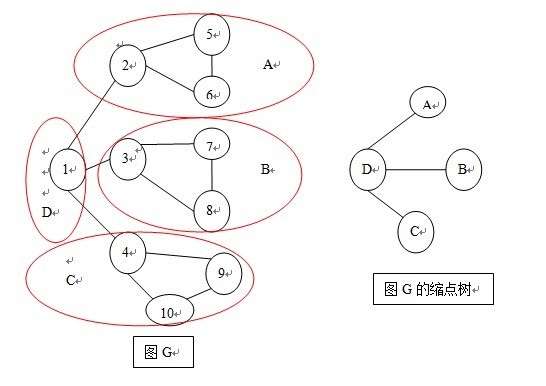
以样例1为例,样例1得到的图G为上左图,
其中Low[4]=Low[9]=Low[10]
Low[3]=Low[7]=Low[8]
Low[2]=Low[5]=Low[6]
Low[1]独自为政....
把Low值相同的点划分为一类,每一类就是一个【边双连通分量】,也就是【缩点】了,不难发现,连接【缩点】之间的边,都是图G的桥,那么我们就得到了上右图以缩点为结点,已桥为树边所构造成的树。
3、 问题再次被转化为“至少在缩点树上增加多少条树边,使得这棵树变为一个双连通图”。
首先知道一条等式:
若要使得任意一棵树,在增加若干条边后,变成一个双连通图,那么
至少增加的边数 =( 这棵树总度数为1的结点数 + 1 )/ 2
(证明就不证明了,自己画几棵树比划一下就知道了)
那么我们只需求缩点树中总度数为1的结点数(即叶子数)有多少就可以了。换而言之,我们只需求出所有缩点的度数,然后判断度数为1的缩点有几个,问题就解决了。
4、 求出所有缩点的度数的方法
两两枚举图G的直接连通的点,只要这两个点不在同一个【缩点】中,那么它们各自所在的【缩点】的度数都+1。注意由于图G时无向图,这样做会使得所有【缩点】的度数都是真实度数的2倍,必须除2后再判断叶子。
===================================================================
附上述知识点的相关传送门,不懂就马上学吧!
有关图论的知识点的定义:http://www.byvoid.com/blog/biconnect/
Tarjan算法入门基础:
http://hi.baidu.com/lydrainbowcat/blog/item/42a6862489c98820c89559f3.html
Tarjan算法应用扩展:
http://hi.baidu.com/lydrainbowcat/blog/item/2194090a96bbed2db1351de8.html
AC代码:
#include<cstdio> #include<cstring> #include<vector> #include<stack> using namespace std; const int N=1e3+10; int n,m,dfn[N],low[N],id[N],pd,sd; vector<int>grap[N]; stack<int>s; bool mark[N]; struct node{ int v,next; }e[N<<1]; int tot,head[N]; int ans,in[N]; void add(int x,int y){ e[++tot].v=y; e[tot].next=head[x]; head[x]=tot; } bool judge(int x,int y){ if((x&1)&&y==x+1) return 1; if(!(x&1)&&y==x-1) return 1; return 0; } void tarjan(int v,int fa){ dfn[v]=low[v]=++pd; s.push(v); mark[v]=1; for(int i=head[v];i;i=e[i].next){ int w=e[i].v; if(judge(i,fa)) continue; if(!dfn[w]){ tarjan(w,i); low[v]=min(low[v],low[w]); } else if(mark[w]){ low[v]=min(low[v],dfn[w]); } } int u; if(dfn[v]==low[v]){ sd++; do{ u=s.top(); s.pop(); id[u]=sd; mark[u]=0; }while(u!=v); } } int main(){ freopen("sh.txt","r",stdin); while(scanf("%d%d",&n,&m)==2){ memset(mark,0,sizeof mark); memset(low,0,sizeof low); memset(dfn,0,sizeof dfn); memset(id,0,sizeof id); memset(in,0,sizeof in); memset(head,0,sizeof head); sd=pd=ans=tot=0; for(int i=1,x,y;i<=m;i++){ scanf("%d%d",&x,&y); add(x,y);add(y,x); } for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,-1); for(int i=1;i<=n;i++){ for(int j=head[i];j;j=e[j].next){ if(id[i]!=id[e[j].v]){ in[id[i]]++; } } } for(int i=1;i<=n;i++) if(in[i]==1) ans++; printf("%d\n",(ans+1)/2); } return 0; }
原文:http://www.cnblogs.com/shenben/p/5961977.html