主题模型TopicModel：LDA中的数学模型

时间：2016-10-21 20:18:58 阅读：318 评论：0 收藏：0 [点我收藏+]

http://blog.csdn.net/pipisorry/article/details/42672935

了解LDA需要明白如下数学原理：

一个函数：gamma函数

四个分布：二项分布、多项分布、beta分布、Dirichlet分布

一个概念和一个理念：共轭先验和贝叶斯框架

两个模型：pLSA、LDA（文档-主题，主题-词语）

一个采样：Gibbs采样

估计未知参数所采用的不同思想：频率学派、贝叶斯学派

皮皮Blog

gamma函数

Gamma函数

Γ (x) = \int \infty 0 t x ? 1 e ? t d t

通过分部积分的方法，可以推导出这个函数有如下的递归性质

Γ (x + 1) = x Γ (x)

于是很容易证明，Γ(x) 函数可以当成是阶乘在实数集上的延拓，具有如下性质

Γ (n) = (n ? 1)!

gamma函数是如何找到的:

1728年，哥德巴赫在考虑数列插值的问题，通俗的说就是把数列的通项公式定义从整数集合延拓到实数集合，例如数列 1,4,9,16,? 可以用通项公式 n2 自然的表达，即便 n 为实数的时候，这个通项公式也是良好定义的。直观的说也就是可以找到一条平滑的曲线y=x2通过所有的整数点(n,n2)，从而可以把定义在整数集上的公式延拓到实数集合。一天哥德巴赫开始处理阶乘序列1,2,6,24,120,720,?,我们可以计算2!,3!, 是否可以计算 2.5!呢？我们把最初的一些(n,n!)的点画在坐标轴上，确实可以看到，容易画出一条通过这些点的平滑曲线。

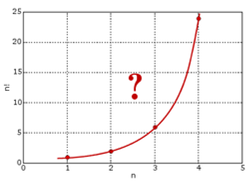
但是哥德巴赫无法解决阶乘往实数集上延拓的这个问题，于是写信请教尼古拉斯.贝努利和他的弟弟丹尼尔.贝努利，由于欧拉当时和丹尼尔.贝努利在一块，他也因此得知了这个问题。而欧拉于1729 年完美的解决了这个问题，由此导致了Γ 函数的诞生。
事实上首先解决n!的插值计算问题的是丹尼尔.贝努利，他发现，如果m,n都是正整数，如果m→∞，有

1 ? 2 ? 3 ? m ( 1 + n ) ( 2 + n ) ? ( m ? 1 + n ) (m + n 2) n ? 1 \to n!

于是用这个无穷乘积的方式可以把

n!的定义延拓到实数集合。例如，取

n=2.5,

m 足够大，基于上式就可以近似计算出

2.5!。

欧拉也偶然的发现 n! 可以用如下的一个无穷乘积表达

[(2 1) n 1 n + 1] [(3 2) n 2 n + 2] [(4 3) n 3 n + 3] ? = n! (?) (1)

用极限形式，这个式子整理后可以写为

lim m \to \infty 1 ? 2 ? 3 ? m ( 1 + n ) ( 2 + n ) ? ( m + n ) (m + 1) n = n! (? ?) (2)

左边可以整理为

= = = 1 ? 2 ? 3 ? m ( 1 + n ) ( 2 + n ) ? ( m + n ) (m + 1) n 1 ? 2 ? 3 ? n ? ( n + 1 ) ( n + 2 ) ? m ( 1 + n ) ( 2 + n ) ? m ? ( m + 1 ) n ( m + 1 ) ( m + 2 ) ? ( m + n ) n! ( m + 1 ) n ( m + 1 ) ( m + 2 ) ? ( m + n ) n! \prod k = 1 n m + 1 m + k \to n! (m \to \infty)

所以 (*)、(**)式都成立。

欧拉开始尝试从一些简单的例子开始做一些计算，看看是否有规律可循，欧拉极其擅长数学的观察与归纳。当 n=1/2 的时候，带入(*)式计算，整理后可以得到

(1 2)! = 2 ? 4 3 ? 3 ? 4 ? 6 5 ? 5 ? 6 ? 8 7 ? 7 ? 8 ? 10 9 ? 9 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? \sqrt

然而右边正好和著名的 Wallis 公式关联。Wallis 在1665年使用插值方法计算半圆曲线

y=x(1?x)???????√ 下的面积(也就是直径为1的半圆面积)的时候，得到关于

π的如下结果，

2 ? 4 3 ? 3 ? 4 ? 6 5 ? 5 ? 6 ? 8 7 ? 7 ? 8 ? 10 9 ? 9 ? = π 4

于是，欧拉利用 Wallis 公式得到了如下一个很漂亮的结果

(1 2)! = π \sqrt 2

欧拉看到

(12)! 中居然有

π, 对数学家而言，有

π 的地方必然有和圆相关的积分。由此欧拉猜测

n! 一定可以表达为某种积分形式，于是欧拉开始尝试把

n! 表达为积分形式。虽然Wallis 的时代微积分还没有发明出来，Wallis 是使用插值的方式做推导计算的，但是Wallis 公式的推导过程基本上就是在处理积分

∫10x12(1?x)12dx，受 Wallis 的启发，欧拉开始考虑如下的一般形式的积分

J (e, n) = \int 10 x e (1 ? x) n d x

此处n 为正整数，

e 为正实数。利用分部积分方法，容易得到

J (e, n) = n e + 1 J (e + 1, n ? 1)

重复使用上述迭代公式，最终可以得到

J (e, n) = 1 ? 2 ? n ( e + 1 ) ( e + 2 ) ? ( e + n + 1 )

于是欧拉得到如下一个重要的式子

n! = (e + 1) (e + 2) ? (e + n + 1) \int 10 x e (1 ? x) n d x

接下来，欧拉使用了一点计算技巧，取

e=f/g 并且令

f→1,g→0,
然后对上式右边计算极限(极限计算的过程此处略去，可见参考文献吧)，于是欧拉得到如下简洁漂亮的结果：

n! = \int 10 (? log t) n d t

欧拉成功的把

n!表达为了积分形式！如果我们做一个变换

t=e?u,就可以得到我们常见的Gamma 函数形式

n! = \int \infty 0 u n e ? u d u

于是,利用上式把阶乘延拓到实数集上，我们就得到 Gamma 函数的一般形式

Γ (x) = \int 10 (? log t) x ? 1 d t = \int \infty 0 t x ? 1 e ? t d t

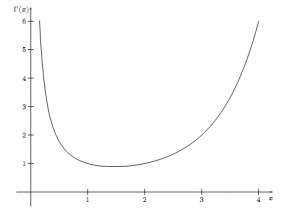
为何 Gamma 函数被定义为 Γ(n)=(n?1)!:

稍微修正一下，把Gamma 函数定义中的 tx?1 替换为tx

Γ (x) = \int \infty 0 t x e ? t d t

这不就可以使得

Γ(n)=n!了嘛。欧拉最早的Gamma函数定义还真是如上所示，选择了

Γ(n)=n!，可是欧拉不知出于什么原因，后续修改了 Gamma 函数的定义，使得

Γ(n)=(n?1)!。而随后勒让德等数学家对Gamma 函数的进一步深入研究中，认可了这个定义，于是这个定义就成为了既成事实。有数学家猜测，一个可能的原因是欧拉研究了如下积分

B (m, n) = \int 10 x m ? 1 (1 ? x) n ? 1 d x

这个函数现在称为Beta 函数。如果Gamma 函数的定义选取满足

Γ(n)=(n?1)!, 那么有

B (m, n) = Γ ( m ) Γ ( n ) Γ ( m + n )

非常漂亮的对称形式。可是如果选取

Γ(n)=n! 的定义，令

E (m, n) = \int 10 x m (1 ? x) n d x

则有

E (m, n) = Γ ( m ) Γ ( n ) Γ ( m + n + 1 )

这个形式显然不如

B(m,n)优美，而数学家总是很在乎数学公式的美感的。

更多的 Gamma 函数的历史，推荐阅读

Philip J. Davis, Leonhard Euler’s Integral: A Historical Profile of the Gamma Function
Jacques Dutka, The Early History of the Factorial Function
Detlef Gronnau, Why is the gamma function so as it is?

more about gamma func：

Gamma 函数欣赏

[火光摇曳]神奇的伽玛函数

从二项分布到Gamma 分布

Gamma 函数在概率统计中频繁现身，包括常见的统计学三大分布(t 分布，χ2 分布，F 分布)、Beta分布、 Dirichlet 分布的密度公式中都有 Gamma 函数的身影；当然发生最直接联系的概率分布是直接由 Gamma 函数变换得到的 Gamma 分布。对Gamma 函数的定义做一个变形，就可以得到如下式子

\int \infty 0 x α ? 1 e ? x Γ ( α ) d x = 1

于是，取积分中的函数作为概率密度，就得到一个形式最简单的Gamma 分布的密度函数

G a m m a (x | α) = x α ? 1 e ? x Γ ( α )

如果做一个变换

x=βt, 就得到Gamma 分布的更一般的形式

G a m m a (t | α, β) = β α t α ? 1 e ? β t Γ ( α )

其中 α称为 shape parameter, 主要决定了分布曲线的形状;而

β称为 rate parameter 或者inverse scale parameter (

1β 称为scale parameter),主要决定曲线有多陡。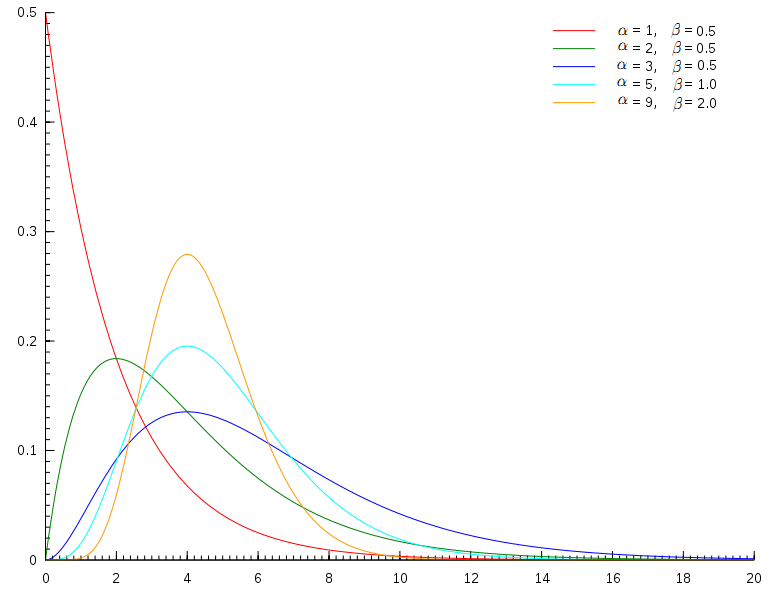

Gamma(t|α,β)分布图像

在概率统计领域，众多统计分布和Gamma 分布有密切关系。指数分布和χ2 分布都是特殊的Gamma 分布。另外Gamma 分布作为先验分布是很强大的，在贝叶斯统计分析中被广泛的用作其它分布的先验。如果把统计分布中的共轭关系类比为人类生活中的情侣关系的话，那指数分布、Poission分布、正态分布、对数正态分布都可以是 Gamma 分布的情人。

接下来的内容中中我们主要关注β=1的简单形式的 Gamma 分布。

Gamma 分布首先和 Poisson 分布、Poisson 过程发生密切的联系。我们容易发现Gamma 分布的概率密度和 Poisson 分布在数学形式上具有高度的一致性。参数为λ的Poisson 分布，概率写为

P o i s s o n (X = k | λ) = λ k e ? λ k !

在 Gamma 分布的密度中取

α=k+1 得到

G a m m a (x | α = k + 1) = x k e ? x Γ ( k + 1 ) = x k e ? x k !

所以这两个分布数学形式上是一致的，只是 Poisson 分布是离散的，Gamma 分布是连续的，可以直观的认为 Gamma 分布是 Poisson 分布在正实数集上的连续化版本。

这种数学上的一致性是偶然的吗？从二项分布出发能把 Gamma 分布和 Poisson 分布紧密联系起来。我们在概率统计中都学过Poisson(λ) 分布可以看成是二项分布 B(n,p) 在 np=λ,n→∞ 条件下的极限分布。如果你对二项分布关注的足够多，可能会知道二项分布的随机变量X～B(n,p)满足如下一个很奇妙的恒等式

P (X \leq k) = n ! k ! ( n ? k ? 1 ) ! \int 1 p t k (1 ? t) n ? k ? 1 d t (?) (1)

这个等式反应的是二项分布和 Beta 分布之间的关系，证明并不难，它可以用一个物理模型直观的做概率解释，而不需要使用复杂的数学分析的方法做证明。由于这个解释和 Beta 分布有紧密的联系，所以这个直观的概率解释我们放到下一个章节，讲解 Beta/Dirichlet 分布的时候进行。此处我们暂时先承认(*)这个等式成立。我们在等式右侧做一个变换t=xn,得到

P (X \leq k) = n ! k ! ( n ? k ? 1 ) ! \int 1 p t k (1 ? t) n ? k ? 1 d t = n ! k ! ( n ? k ? 1 ) ! \int n n p (x n) k (1 ? x n) n ? k ? 1 d x n = ( n ? 1 ) ! k ! ( n ? k ? 1 ) ! \int n n p (x n) k (1 ? x n) n ? k ? 1 d x = \int n n p (n ? 1 k) (x n) k (1 ? x n) n ? k ? 1 d x = \int n n p B i n o m i a l (Y = k | n ? 1, x n) d x (2)

上式左侧是二项分布

B(n,p), 而右侧为无穷多个二项分布

B(n?1,xn)的积分和, 所以可以写为

B i n o m i a l (X \leq k | n, p) = \int n n p B i n o m i a l (Y = k | n ? 1, x n) d x (3)

实际上，对上式两边在条件

np=λ,n→∞ 下取极限，则左边有

B(n,p)→Poisson(λ), 而右边有

B(n?1,xn)→Poisson(x),所以得到

P o i s s o n (X \leq k | λ) = \int \infty λ P o i s s o n (Y = k | x) d x (4)

把上式右边的Possion 分布展开，于是得到

P o i s s o n (X \leq k | λ) = \int \infty λ P o i s s o n (Y = k | x) d x = \int \infty λ x k e ? x k ! d x

所以对于们得到如下一个重要而有趣的等式

P o i s s o n (X \leq k | λ) = \int \infty λ x k e ? x k ! d x (? ?) (5)

接下来我们继续玩点好玩的，对上边的等式两边在 λ→0 下取极限，左侧Poisson分布是要至少发生k个事件的概率， λ→0 的时候就不可能有事件发生了，所以 P(X≤k)→1, 于是我们得到

1 = lim λ \to 0 \int \infty λ x k e ? x k ! d x = \int \infty 0 x k e ? x k ! d x

在这个积分式子说明

f(x)=xke?xk!在正实数集上是一个概率分布函数，而这个函数恰好就是Gamma 分布。我们继续把上式右边中的

k! 移到左边，于是得到

k! = \int \infty 0 x k e ? x d x

于是我们得到了

k! 表示为积分的方法。

看，我们从二项分布的一个等式出发, 同时利用二项分布的极限是Possion 分布这个性质，基于比较简单的逻辑，推导出了 Gamma 分布，同时把 k! 表达为 Gamma 函数了！实际上以上推导过程是给出了另外一种相对简单的发现 Gamma 函数的途径。

回过头我们看看(**)式,非常有意思，它反应了Possion 分布和 Gamma 分布的关系，这个和(*)式中中反应的二项分布和Beta 分布的关系具有完全相同的结构。把(**)式变形一下得到

P o i s s o n (X \leq k | λ) + \int λ 0 x k e ? x k ! d x = 1

我们可以看到，Poisson分布的概率累积函数和Gamma 分布的概率累积函数有互补的关系。

其实(*)和(**)这两个式子都是陈希儒院士的《概率论与数理统计》这本书第二章的课后习题，不过陈老师习题答案中给的证明思路是纯粹数学分析的证明方法，虽然能证明等式成立，但是看完证明后无法明白这两个等式是如何被发现的。上诉的论述过程说明，从二项分布出发，这两个等式都有可以很好的从概率角度进行理解。

皮皮Blog

Bet/Dirichlet分布

魔鬼的游戏—认识Beta 分布

统计学就是猜测上帝的游戏,当然我们不总是有机会猜测上帝，运气不好的时候就得揣度魔鬼的心思。有一天你被魔鬼撒旦抓走了，撒旦说：”我有一个魔盒，上面有一个按钮，你每按一下按钮，就均匀的输出一个[0,1]之间的随机数，我现在按10下，我手上有10个数，你猜第7大的数是什么，偏离不超过0.01就算对。“ 你应该怎么猜呢？

从数学的角度抽象一下，上面这个游戏其实是在说随机变量X1,X2,?,Xn～iidUniform(0,1)，把这n 个随机变量排序后得到顺序统计量 X(1),X(2)，?,X(n), 然后问 X(k) 的分布是什么。

在概率统计学中，均匀分布应该算得上是潘多拉魔盒，几乎所有重要的概率分布都可以从均匀分布Uniform(0,1)中生成出来;尤其是在统计模拟中，所有统计分布的随机样本都是通过均匀分布产生的。

对于上面的游戏而言 n=10,k=7, 如果我们能求出 X(7) 的分布的概率密度，那么用概率密度的极值点去做猜测就是最好的策略。对于一般的情形，X(k) 的分布是什么呢？那我们尝试计算一下X(k) 落在一个区间 [x,x+Δx] 的概率，也就是求如下概率值

P (x \leq X (k) \leq x + Δ x) = ?

把 [0,1] 区间分成三段 [0,x),[x,x+Δx],(x+Δx,1],我们先考虑简单的情形，假设n 个数中只有一个落在了区间 [x,x+Δx]内，则因为这个区间内的数X(k)是第k大的，则[0,x)中应该有k?1 个数，(x,1] 这个区间中应该有n?k 个数。不失一般性，我们先考虑如下一个符合上述要求的事件E

E = {X 1 \in [x, x + Δ x], X i \in [0, x) (i = 2, ?, k), X j \in (x + Δ x, 1] (j = k + 1, ?, n)}

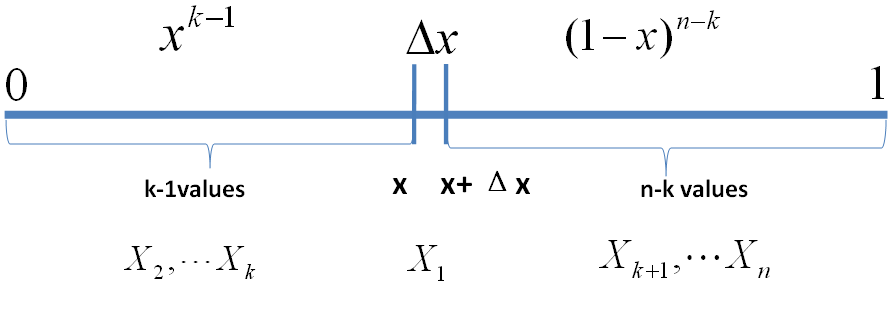
事件 E

则有

P (E) = \prod i = 1 n P (X i) = x k ? 1 (1 ? x ? Δ x) n ? k Δ x = x k ? 1 (1 ? x) n ? k Δ x + o (Δ x)

o(Δx)表示Δx的高阶无穷小。显然，由于不同的排列组合，即n个数中有一个落在[x,x+Δx]区间的有n种取法，余下n?1个数中有k?1个落在[0,x)的有(n?1k?1)种组合，所以和事件E等价的事件一共有n(n?1k?1)个。继续考虑稍微复杂一点情形，假设n 个数中有两个数落在了区间 [x,x+Δx]，

E' = {X 1, X 2 \in [x, x + Δ x], X i \in [0, x) (i = 3, ?, k), X j \in (x + Δ x, 1] (j = k + 1, ?, n)}

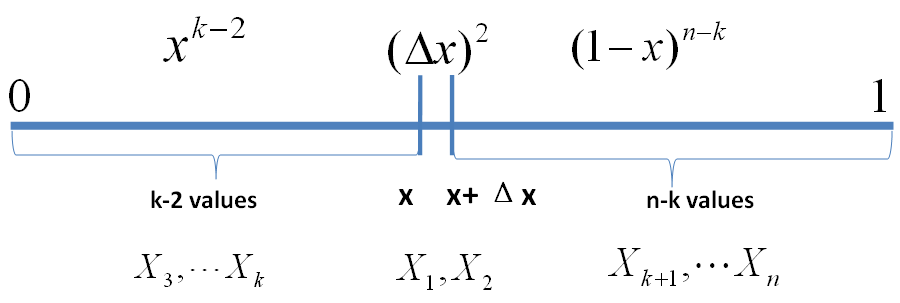
事件E’

则有

P (E') = x k ? 2 (1 ? x ? Δ x) n ? k (Δ x) 2 = o (Δ x)

从以上分析我们很容易看出，只要落在[x,x+Δx]内的数字超过一个，则对应的事件的概率就是o(Δx)。于是

P (x \leq X (k) \leq x + Δ x) = n (n ? 1 k ? 1) P (E) + o (Δ x) = n (n ? 1 k ? 1) x k ? 1 (1 ? x) n ? k Δ x + o (Δ x)

所以，可以得到

X(k)的概率密度函数为

f (x) = lim Δ x \to 0 P ( x \leq X ( k ) \leq x + Δ x ) Δ x = n (n ? 1 k ? 1) x k ? 1 (1 ? x) n ? k = n ! ( k ? 1 ) ! ( n ? k ) ! x k ? 1 (1 ? x) n ? k x \in [0, 1]

利用Gamma 函数，我们可以把

f(x) 表达为

f (x) = Γ ( n + 1 ) Γ ( k ) Γ ( n ? k + 1 ) x k ? 1 (1 ? x) n ? k

还记得神奇的 Gamma 函数可以把很多数学概念从整数集合延拓到实数集合吧。我们在上式中取α=k,β=n?k+1, 于是我们得到

f (x) = Γ ( α + β ) Γ ( α ) Γ ( β ) x α ? 1 (1 ? x) β ? 1 (1)

这个就是一般意义上的 Beta 分布！可以证明，在

α,β取非负实数的时候，这个概率密度函数也都是良定义的。

回到魔鬼的游戏，这n=10,k=7这个具体的实例中，我们按照如下密度分布的峰值去猜测才是最有把握的。

f (x) = 10 ! ( 6 ) ! ( 3 ) ! x 6 (1 ? x) 3 x \in [0, 1]

Beta-Binomial 共轭

然而即便如此，我们能做到一次猜中的概率也不高，很不幸，你第一次没有猜中，魔鬼说：“我再仁慈一点，再给你一个机会，你按5下这个机器，你就得到了5个[0,1]之间的随机数，然后我可以告诉你这5个数中的每一个，和我的第7大的数相比，谁大谁小，然后你继续猜我手头的第7大的数是多少。”这时候我们应该怎么猜测呢？

魔鬼的第二个题目，数学上形式化一下，就是

X1,X2,?,Xn～iidUniform(0,1)，对应的顺序统计量是X(1),X(2)，?,X(n), 我们要猜测 p=X(k)；
Y1,Y2,?,Ym～iidUniform(0,1),Yi中有m1个比p小，m2个比p大；
问 P(p|Y1,Y2,?,Ym) 的分布是什么。

由于p=X(k)在X1,X2,?,Xn中是第k大的，利用Yi的信息，我们容易推理得到p=X(k) 在X1,X2,?,Xn,Y1,Y2,?,Ym～iidUniform(0,1) 这(m+n)个独立随机变量中是第k+m1大的，于是按照上一个小节的推理，此时p=X(k) 的概率密度函数是 Beta(p|k+m1,n?k+1+m2)。按照贝叶斯推理的逻辑，我们把以上过程整理如下：

p=X(k)是我们要猜测的参数，我们推导出p 的分布为 f(p)=Beta(p|k,n?k+1),称为p 的先验分布；
数据Yi中有m1个比p小，m2个比p大，Yi相当于是做了m次贝努利实验，所以m1 服从二项分布 B(m,p)；
在给定了来自数据提供的(m1,m2)的知识后，p 的后验分布变为 f(p|m1,m2)=Beta(p|k+m1,n?k+1+m2)

我们知道贝叶斯参数估计的基本过程是

先验分布 + 数据的知识 = 后验分布

以上贝叶斯分析过程的简单直观的表述就是

B e t a (p | k, n ? k + 1) + C o u n t (m 1, m 2) = B e t a (p | k + m 1, n ? k + 1 + m 2)

其中 (m1,m2) 对应的是二项分布B(m1+m2,p)的计数。更一般的，对于非负实数

α,β，我们有如下关系

B e t a (p | α, β) + C o u n t (m 1, m 2) = B e t a (p | α + m 1, β + m 2) (1)

这个式子实际上描述的就是 Beta-Binomial 共轭，此处共轭的意思就是，数据符合二项分布的时候，参数的先验分布和后验分布都能保持Beta 分布的形式，这种形式不变的好处是，我们能够在先验分布中赋予参数很明确的物理意义，这个物理意义可以延续到后验分布中进行解释，同时从先验变换到后验过程中从数据中补充的知识也容易有物理解释。

而我们从以上过程可以看到，Beta 分布中的参数α,β都可以理解为物理计数，这两个参数经常被称为伪计数(pseudo-count)。

基于以上逻辑，我们也可以把Beta(p|α,β)写成下式来理解
Beta(p|1,1)+Count(α?1,β?1)=Beta(p|α,β) (???) 其中 Beta(p|1,1) 恰好就是均匀分布Uniform(0,1)。

对于(***) 式，我们其实也可以纯粹从贝叶斯的角度来进行推导和理解。假设有一个不均匀的硬币抛出正面的概率为p,抛m次后出现正面和反面的次数分别是m1,m2，那么按传统的频率学派观点，p的估计值应该为p?=m1m。而从贝叶斯学派的观点来看，开始对硬币不均匀性一无所知，所以应该假设p～Uniform(0,1), 于是有了二项分布的计数(m1,m2)
之后，按照贝叶斯公式如下计算p 的后验分布

P (p | m 1, m 2) = P ( p ) ? P ( m 1 , m 2 | p ) P ( m 1 , m 2 ) = 1 ? P ( m 1 , m 2 | p ) \int 1 0 P ( m 1 , m 2 | t ) d t = ( m m 1 ) p m 1 ( 1 ? p ) m 2 \int 1 0 ( m m 1 ) t m 1 ( 1 ? t ) m 2 d t = p m 1 ( 1 ? p ) m 2 \int 1 0 t m 1 ( 1 ? t ) m 2 d t

计算得到的后验分布正好是

Beta(p|m1+1,m2+1)。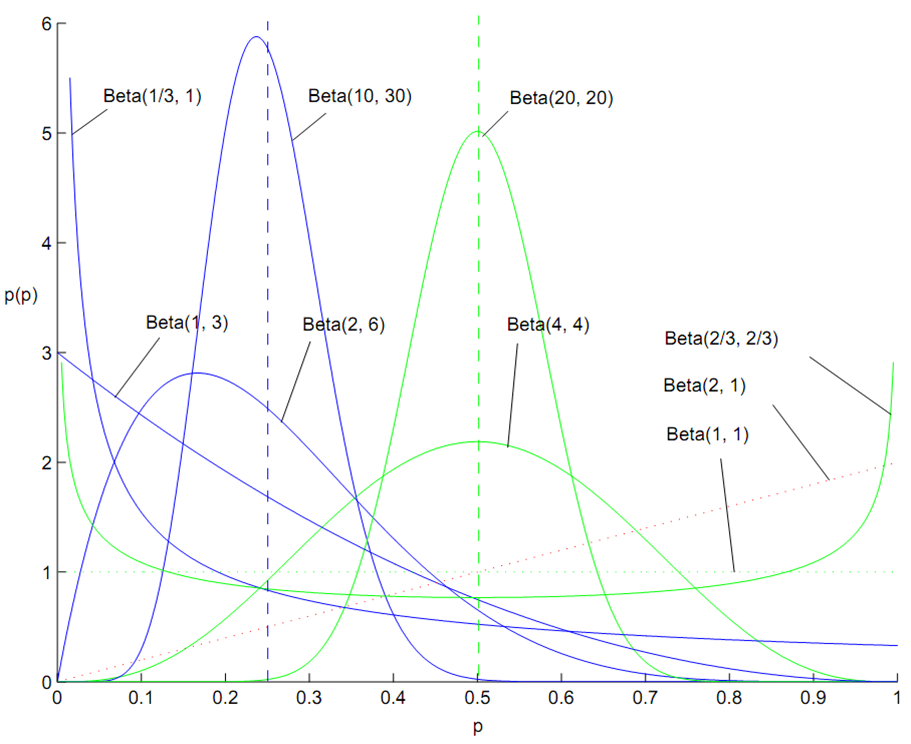

百变星君Beta分布

{Beta(1, 1)就是均匀分布}

Beta 分布的概率密度我们把它画成图，会发现它是个百变星君，它可以是凹的、凸的、单调上升的、单调下降的；可以是曲线也可以是直线，而均匀分布也是特殊的Beta分布。由于Beta 分布能够拟合如此之多的形状，因此它在统计数据拟合中被广泛使用。

在上一个小节中，我们从二项分布推导Gamma 分布的时候，使用了如下的等式

P (C \leq k) = n ! k ! ( n ? k ? 1 ) ! \int 1 p t k (1 ? t) n ? k ? 1 d t, C ～ B (n, p) (2)

现在大家可以看到，左边是二项分布的概率累积，右边实际上是

Beta(t|k+1,n?k) 分布的概率积分。这个式子在上一小节中并没有给出证明，下面我们利用和魔鬼的游戏类似的概率物理过程进行证明。

我们可以如下构造二项分布，取随机变量 X1,X2,?,Xn～iidUniform(0,1),一个成功的贝努利实验就是Xi<p,否则表示失败,于是成功的概率为p。C用于计数成功的次数，于是C～B(n,p)。

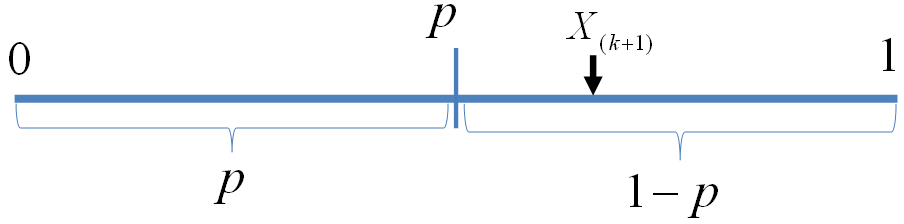
贝努利实验最多成功k次

显然我们有如下式子成立

P (C \leq k) = P (X (k + 1) > p)

此处X(k+1)是顺序统计量，为第k+1大的数。等式左边表示贝努利实验成功次数最多k次，右边表示第k+1 大的数必然对应于失败的贝努利实验，从而失败次数最少是n?k次，所以左右两边是等价的。由于X(k+1)～Beta(t|k+1,n?k), 于是

P (C \leq k) = P (X (k + 1) > p) = \int 1 p B e t a (t | k + 1, n ? k) d t = n ! k ! ( n ? k ? 1 ) ! \int 1 p t k (1 ? t) n ? k ? 1 d t

最后我们再回到魔鬼的游戏，如果你按出的5个随机数字中，魔鬼告诉你有2个小于它手中第7大的数，那么你应该
按照如下概率分布的峰值做猜测是最好的

B e t a (x | 9, 7) = 15 ! ( 8 ) ! ( 6 ) ! x 8 (1 ? x) 6 x \in [0, 1]

皮皮Blog

Dirichlet分布

很幸运的，你这次猜中了，魔鬼开始甩赖了：这个游戏对你来说太简单了，我要加大点难度，我们重新来一次，我按魔盒20下生成20个随机数，你同时给我猜第7大和第13大的数是什么，这时候应该如何猜测呢？

数学形式化如下：

X1,X2,?,Xn～iidUniform(0,1)，
排序后对应的顺序统计量 X(1),X(2)，?,X(n),
问 (X(k1),X(k1+k2))的联合分布是什么；

完全类似于第一个游戏的推导过程，我们可以进行如下的概率计算(为了数学公式的简洁对称，我们取x3满足x1+x2+x3=1,但只有x1,x2是变量)

(X(k1),X(k1+k2))的联合分布推导

P (X (k 1) \in (x 1, x 1 + Δ x), X (k 1 + k 2) \in (x 2, x 2 + Δ x)) = n (n ? 1) (n ? 2 k 1 ? 1 , k 2 ? 1) x k 1 ? 1 1 x k 2 ? 1 2 x n ? k 1 ? k 2 3 (Δ x) 2 = n ! ( k 1 ? 1 ) ! ( k 2 ? 1 ) ! ( n ? k 1 ? k 2 ) ! x k 1 ? 1 1 x k 2 ? 1 2 x n ? k 1 ? k 2 3 (Δ x) 2

于是我们得到

(X(k1),X(k1+k2))的联合分布是

f (x 1, x 2, x 3) = n ! ( k 1 ? 1 ) ! ( k 2 ? 1 ) ! ( n ? k 1 ? k 2 ) ! x k 1 ? 1 1 x k 2 ? 1 2 x n ? k 1 ? k 2 3 = Γ ( n + 1 ) Γ ( k 1 ) Γ ( k 2 ) Γ ( n ? k 1 ? k 2 + 1 ) x k 1 ? 1 1 x k 2 ? 1 2 x n ? k 1 ? k 2 3

这个分布其实就是3维形式的 Dirichlet 分布

Dir(x1,x2,x3|k1,k2,n?k1?k2+1)。令α1=k1,α2=k2,α3=n?k1?k2+1,于是分布密度可以写为

f (x 1, x 2, x 3) = Γ ( α 1 + α 2 + α 3 ) Γ ( α 1 ) Γ ( α 2 ) Γ ( α 3 ) x α 1 ? 1 1 x α 2 ? 1 2 x α 3 ? 1 3 (1)

即便 α→=(α1,α2,α3) 延拓到非负实数集合，以上概率分布也是良定义的。

从形式上我们也能看出，Dirichlet 分布是Beta 分布在高维度上的推广，他和Beta 分布一样也是一个百变星君，密度函数可以展现出多种形态。

不同α 下的Dirichlet 分布

{ {αk} = 1时相当于高维均匀分布 -}

Dirichlet-Multinomial 共轭

类似于魔鬼的游戏2，我们也可以调整一下游戏3，从魔盒中生成m个随机数Y1,Y2,?,Ym～iidUniform(0,1) 并让魔鬼告诉我们Yi和(X(k1),X(k1+k2))相比谁大谁小。于是有如下游戏4

X1,X2,?,Xn～iidUniform(0,1)，排序后对应的顺序统计量X(1),X(2)，?,X(n)
令p1=X(k1),p2=X(k1+k2),p3=1?p1?p2(加上p3是为了数学表达简洁对称),我们要猜测p→=(p1,p2,p3)；
Y1,Y2,?,Ym～iidUniform(0,1),Yi中落到[0,p1),[p1,p2),[p2,1] 三个区间的个数分别为 m1,m2,m3，m=m1+m2+m3；
问后验分布 P(p→|Y1,Y2,?,Ym) 的分布是什么。

为了方便，我们记

m \to = (m 1, m 2, m 3), k \to = (k 1, k 2, n ? k 1 ? k 2 + 1)

由游戏中的信息，我们可以推理得到

p1,p2在

X1,X2,?,Xn,

Y1,Y2,?,Ym

～iidUniform(0,1)这

m+n个数中分别成为了第

k1+m1,k2+m2大的数，于是后验分布

P(p→|Y1,Y2,?,Ym) 应该是

Dir(p→|k1+m1,k1+m2,n?k1?k2+1+m3),即

Dir(p→|k→+m→)。按照贝叶斯推理的逻辑，我们同样可以把以上过程整理如下：

我们要猜测参数 p→=(p1,p2,p3)，其先验分布为Dir(p→|k→)；
数据Yi落到[0,p1),[p1,p2),[p2,1]三个区间的个数分别为m1,m2,m3，所以m→=(m1,m2,m3) 服从多项分布Mult(m→|p→)
在给定了来自数据提供的知识m→后，p→ 的后验分布变为 Dir(p→|k→+m→)

以上贝叶斯分析过程的简单直观的表述就是

D i r (p \to | k \to) + M u l t C o u n t (m \to) = D i r (p \to | k \to + m \to)

令

α→=k→,把

α→从整数集合延拓到实数集合，更一般的可以证明有如下关系

D i r (p \to | α \to) + M u l t C o u n t (m \to) = D i r (p | α \to + m \to) (2)

以上式子实际上描述的就是 Dirichlet-Multinomial 共轭，而我们从以上过程可以看到，Dirichlet 分布中的参数α→都可以理解为物理计数。

类似于 Beta 分布，我们也可以把 Dir(p→|α→)作如下分解

D i r (p \to | 1 \to) + M u l t C o u n t (m \to ? 1 \to) = D i r (p \to | α \to)

此处

1→=(1,1,?,1)。自然，上式我们也可以类似地用纯粹贝叶斯的观点进行推导和解释。

以上的游戏我们还可以往更高的维度上继续推，譬如猜测 X(1),X(2)，?,X(n) 中的4、5、…等更多个数，于是就得到更高纬度的 Dirichlet 分布和 Dirichlet-Multinomial 共轭。一般形式的 Dirichlet 分布定义如下

D i r (p \to | α \to) = Γ ( \sum K k = 1 α k ) \prod K k = 1 Γ ( α k ) \prod k = 1 K p α k ? 1 k (3)

对于给定的

p→和

N,多项分布定义为

M u l t (n \to | p \to, N) = (N n \to) \prod k = 1 K p n k k (4)

而

Mult(n→|p→,N) 和

Dir(p→|α→)这两个分布是共轭关系。

Beta/Dirichlet 分布的一个性质

如果 p～Beta(t|α,β), 则

E (p) = \int 10 t ? B e t a (t | α, β) d t = \int 10 t ? Γ ( α + β ) Γ ( α ) Γ ( β ) t α ? 1 (1 ? t) β ? 1 d t = Γ ( α + β ) Γ ( α ) Γ ( β ) \int 10 t α (1 ? t) β ? 1 d t

上式右边的积分对应到概率分布

Beta(t|α+1,β)，对于这个分布，我们有

\int 10 Γ ( α + β + 1 ) Γ ( α + 1 ) Γ ( β ) t α (1 ? t) β ? 1 d t = 1

把上式带入

E(p)的计算式，得到

E (p) = Γ ( α + β ) Γ ( α ) Γ ( β ) ? Γ ( α + 1 ) Γ ( β ) Γ ( α + β + 1 ) = Γ ( α + β ) Γ ( α + β + 1 ) Γ ( α + 1 ) Γ ( α ) = α α + β (5)

这说明，对于Beta 分布的随机变量，其均值可以用αα+β来估计。

Dirichlet 分布也有类似的结论，如果p→～Dir(t→|α→)，同样可以证明

E (p \to) = (α 1 \sum K i = 1 α i, α 2 \sum K i = 1 α i, ?, α K \sum K i = 1 α i) (6)

{通过一个游戏来解释这两个共轭关系，主要是想说明这个共轭关系是可以对应到很具体的概率物理过程的}

Dirichlet 分布

根据wikipedia上的介绍，维度K ≥ 2（x1,x2…xK-1维，共K个）的狄利克雷分布在参数α1, ..., αK > 0上、基于欧几里得空间RK-1里的勒贝格测度有个概率密度函数，定义为：

其中，技术分享相当于是多项beta函数

且技术分享

此外，x1+x2+…+xK-1+xK=1，x1,x2…xK-1>0，且在(K-1)维的单纯形上，其他区域的概率密度为0。

当然，也可以如下定义Dirichlet 分布

其中的技术分享称为Dirichlet 分布的归一化系数：

且根据Dirichlet分布的积分为1（概率的基本性质），可以得到：

将Dirichlet分布的概率密度函数取对数，绘制对称Dirichlet分布的图像如下图所示：

上图中，取K=3，也就是有两个独立参数x1,x2，分别对应图中的两个坐标轴，第三个参数始终满足x3=1-x1-x2且α1=α2=α3=α，图中反映的是参数α从α=(0.3, 0.3, 0.3)变化到(2.0, 2.0, 2.0)时的概率对数值的变化情况。

皮皮Blog

共轭先验分布

由于有积分的存在，贝叶斯估计常常会很难推算，这里我们就需要利用一种共轭先验(Conjugate Prior)的数学知识。
什么是共轭呢？轭的意思是束缚、控制，共轭从字面上理解，则是共同约束，或互相约束。

在贝叶斯统计理论中，如果某个随机变量 ? 的先验分布 p(?) 和后验分布 p(?|X) 属于统一分布簇(也就是说有同样的函数形式)，则称先验分布 p(?) 和后验分布 p(?|X) 为共轭分布，先验分布 p(?) 是似然函数 p(X|?) 的共轭先验。也就是在贝叶斯概率理论中，如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律，那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

比如，某观测数据服从概率分布P(θ)时，当观测到新的X数据时，我们一般会遇到如下问题：

可否根据新观测数据X，更新参数θ？
根据新观测数据可以在多大程度上改变参数θ，即

当重新估计θ的时候，给出新参数值θ的新概率分布，即P(θ|x)。

事实上，根据根据贝叶斯公式可知：

举个例子。投掷一个非均匀硬币，可以使用参数为θ的伯努利模型，θ为硬币为正面的概率，那么结果x的分布形式为：

其共轭先验为beta分布，具有两个参数技术分享

和

，称为超参数（hyperparameters）。且这两个参数决定了θ参数，其Beta分布形式为

然后计算后验概率

归一化这个等式后会得到另一个Beta分布，从而证明了Beta分布确实是伯努利分布的共轭先验分布。

由于pLSA中参数 Φ和Θ 都服从多项分布，因此选择Dirichlet分布作为他们的共轭先验。在pLSA中，假设这俩多项分布是确定的，我们在已经假设确定的分布下，选择具体的主题和词项；但在LDA中，这俩多项分布的参数是被当作随机变量，服从另一层先验分布，所以，Dirichlet分布也称作分布的分布，其定义如下：

D i r (p ? | α ?) ? Γ ( \sum K k = 1 α k ) \prod K k = 1 Γ ( α k ) \prod k = 1 K p α k ? 1 k ? 1 Δ ( α ? ) \prod k = 1 K p α k ? 1 k (1)

其中， p? 是要猜测的随机向量，α? 是超参数， Δ(α? ) 称作Delta函数，可以看作Beta函数的多项式扩展，是Dirichlet分布的归一化系数，定义如下：

Δ (α ?) = \prod d i m α ? k = 1 Γ ( α k ) Γ ( \sum d i m α ? k = 1 α k ) = i n t \prod k = 1 V p α k ? 1 k d p ? (2)

相应的多项分布定义：

M u l t (n ? | p ?, N) ? (N n ?) \prod k = 1 K p n k k (3)

其中， p? 和n? 服从约束 ∑kpk=1 和 ∑knk=N 。由于 Γ(x+1)=x! 就是阶乘在实数集上的扩展，显然，公式(1)和(3)有相同的形式，所以，这俩分布也称作Dirichlet-Multinomail共轭。

如果 p? ～Dir(p? |α? )，则p? 中的任一元素 pi 的期望是：

E (p i) = \int 10 p i ? D i r (p ? | α ?) d p = Γ ( \sum K k = 1 α k ) Γ ( α i ) ? Γ ( α i + 1 ) Γ ( \sum K k = 1 α k + 1 ) = α i \sum K k = 1 α k (4)

可以看出，超参数 αk的直观意义就是事件先验的伪计数(prior pseudo-count)。

高斯分布的共轭分布

高斯分布的贝叶斯推理

本节的重点是，如果用贝叶斯理论估计高斯分布的均值或方差，需要选择哪些分布作为共轭先验。

单变量高斯分布

（1）方差已知，估计均值：

似然函数是：

共轭先验是：

后验分布是：

即：

其中：

（2）均值已知，估计方差：

似然函数是：

共轭先验是Gamma分布：技术分享

后验分布是：

（3）均值和期望未知：

共轭分布为高斯伽马分布（Gaussian-gamma distribution）：技术分享

多变量高斯分布

（1）方差已知，估计均值，采用的共轭先验还是高斯分布；

（2）均值已知，方差未知，采用Wishart分布：技术分享

（3）均值和方差都未知，采用Gaussian-Wishart分布：技术分享

[模式识别与机器学习（二）：常用的概率分布（共轭分布等） ]

皮皮Blog

总结

1.首先了解gamma函数：由问题n！中n为实数推导出Gamma函数

Γ (x) = \int \infty 0 t x ? 1 e ? t d t

2.了解二项、多项分布，从二项分布中推导出gamma分布
3.魔鬼的第1个游戏 [均匀输出[0,1]之间的随机数10次，猜第7大的数] 推导出beta分布
4.魔鬼的第2个游戏 [没猜中，再按5下这个机器得到了5个[0,1]之间的随机数，告诉你这5个数和我的第7大的数相比，谁大谁小，然后继续猜第7大的数]
推导出beta-binominal共轭Beta(p|k,n?k+1)+Count(m1,m2)=Beta(p|k+m1,n?k+1+m2)
5.魔鬼的第3个游戏 [重新来一次，按魔盒20下生成20个随机数，同时猜第7大和第13大的数] 推导出Dirichlet分布
6.魔鬼的第4个游戏 [从魔盒中生成

m个随机数