现在给出一个Web统计信息,他们存储着每小时的访问次数。每一行包含连续的小时和信息,以及该小时Web的访问次数。现在要解决的问题是,估计在何时访问量达到基础设施的极限。极限数据是每小时100000次访问。
1.读取数据:
# 获取数据 filepath = r‘C:\Users\TD\Desktop\data\Machine Learning\1400OS_01_Codes\data\web_traffic.tsv‘ data = sp.genfromtxt(filepath,delimiter = ‘\t‘) x = data[:,0] y = data[:,1]
其中,x表示小时,y表示访问量。
2.预处理和清洗数据:
print sp.sum(sp.isnan(y))
结果显示含有8个控值,为了方便,在此处理缺失值办法是直接剔除。
x = x[~sp.isnan(y)] y = y[~sp.isnan(y)]
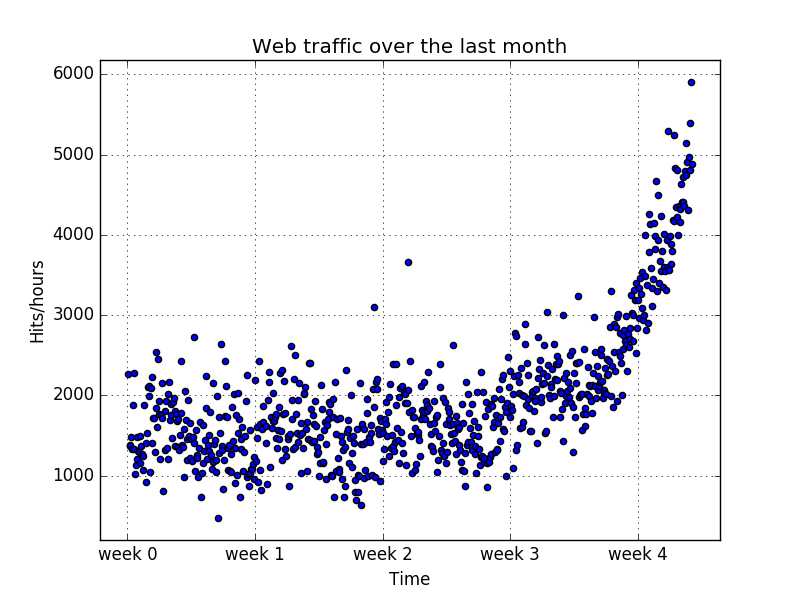
接下来,画出散点图,观察数据的规律:
# 可视化,观察数据规律
plt.scatter(x,y)
plt.title(‘Web traffic over the last month‘)
plt.xlabel(‘Time‘)
plt.ylabel(‘Hits/hours‘)
plt.xticks([w*24*7 for w in range(5)],
[‘week {}‘.format(i) for i in range(5)])
plt.autoscale(tight = True)
plt.grid()
plt.show()
3 选择正确的模型和学习算法:
回答原始问题需要明确以下几点:
1)找到噪声数据后真正的模型
2)使用这个模型预测未来,一遍解决我们的问题
1.首先需要明白模型与实际数据区别。模型可以理解为对复杂现实世界简化的理论近似。它总会包含一些劣质的类容,这个就叫做近似误差。我们用真实数据与模型预测的数据之间的平方距离来计算这个误差,对于一个训练好的模型f,按照下面函数来计算误差:
def error(f,x,y): return sp.sum((f(x)-y)**2)
原文:http://www.cnblogs.com/td15980891505/p/5996062.html