另一篇介绍的很好deblog:http://blog.jobbole.com/71431/
PageRank 是对搜索引擎的搜索网页进行排序的算法。
过去的排序算法是比如使用网页名字,关键词出现的次数,人工等方法,但是这种方法一方面搜索结果不准确,另一方面搜索结果容易被人为因素影响。
所以,PageRank应运而生。
PageRank算法计算每一个网页的PageRank值,然后根据这个值的大小对网页的重要性进行排序。它的思想是模拟一个悠闲的上网者,上网者首先随机选择一个网页打开,然后在这个网页上呆了几分钟后,跳转到该网页
所指向的链接,这样无所事事、漫无目的地在网页上跳来跳去,PageRank就是估计这个悠闲的上网者分布在各个网页上的概率。
PageRank背后的两个基本假设:
二、PageRank模型
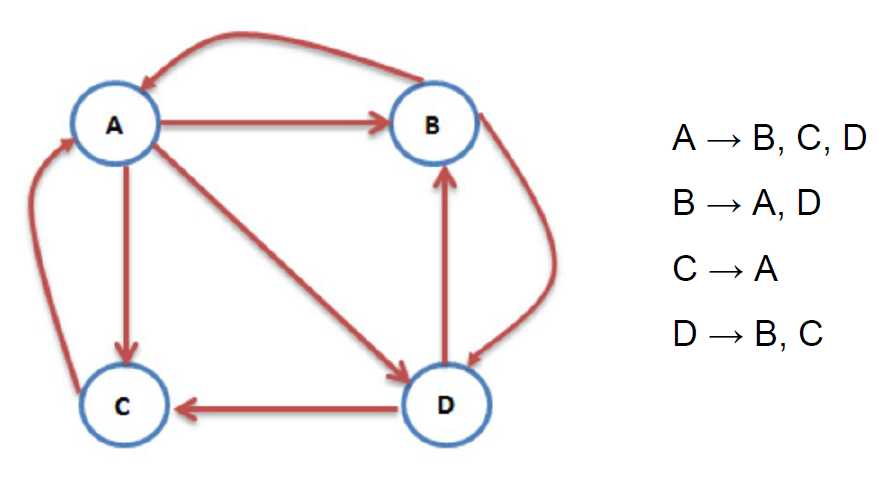
互联网中网页和网页之间的链接关系组成一个有向图,其中网页是节点,网页之间的链接为有相边。如上图所示的模型就表示四个网页,A指向B的箭头表示A中存在指向B的链接。
可以使用转移矩阵来表示这样一个有向图。上图所对应的模型即可用转移矩阵表示为:
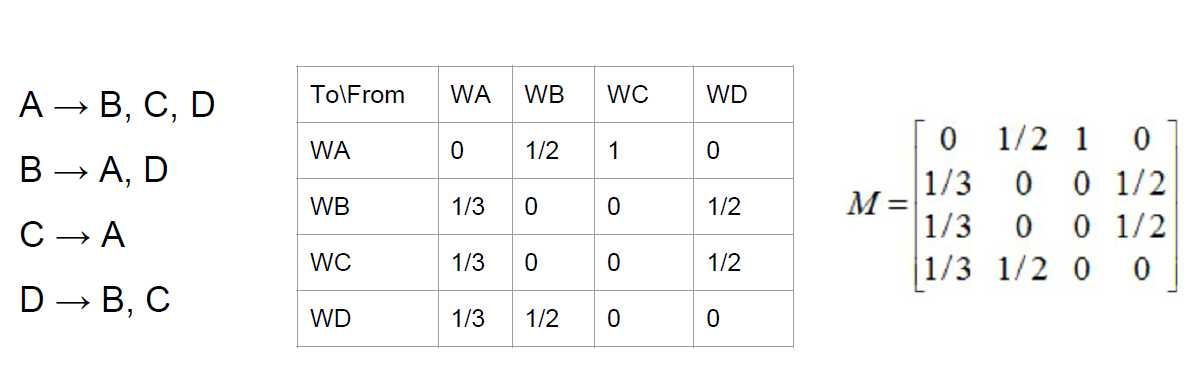
我们看到,A网页发出三个链接,那么到任何一个网页的概率都均等,所以我们上边的矩阵A这一列对用的BCD三个网页概率都为1/3。
有了上面的转移矩阵,我们从两个角度来思考:
一方面,一个网页X如果有许多网页指向他,那么转移矩阵的X行就会有许多的非零元素,转移之后这个网页就会获得更大的PageRank,这刚好和我们上文提到的数量假设相对应。
另一方面,假设X网页具有很高的重要性,那么X所转移到的那些网页将会由于X的高重要性而获得相对更高的重要性,这刚好和我们上文提到的质量假设相对应。
那么,怎样表示一个网页的重要性呢?
我们使用PageRank Matrix来表示。上述有向图对应一个4 * 1的PageRank矩阵。
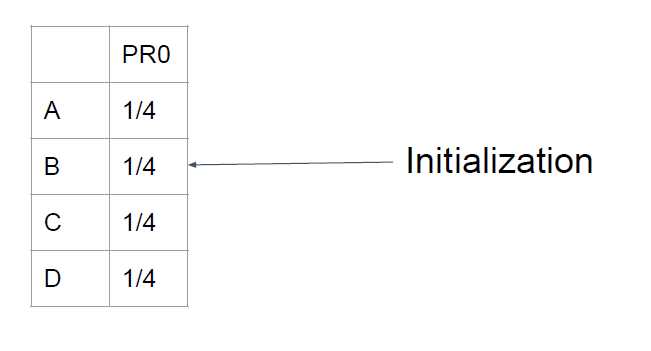
为什么初始化为均分初始化呢?我们可以这样思考,一个无聊的上网这开始想要来打开一个网页,那么他打开这一堆网页中的任何一个在最开始都是风概率的。(当然不考虑个人信息,那是个性化搜索的范畴)
好了,我们现在有了两个矩阵,转移矩阵和初始的PageRank矩阵PR0, 我们接下来就要模拟网页间的跳转。
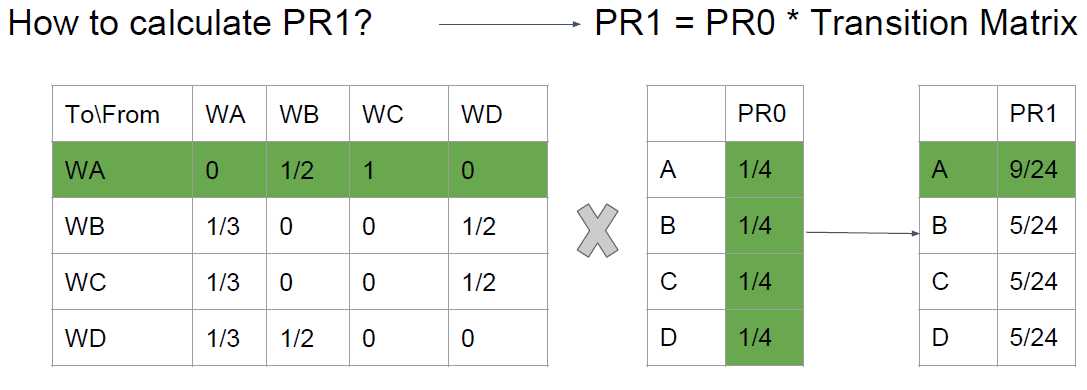
如图,一次跳转之后,网页A的PageRank就应该由可以跳到A的网页和他们各自的PageRank相乘之后的和来表示。上图的矩阵乘法就可以表示一次跳转之后的各个网页的PageRank值。
同理,PR2 = Transition Matrix * PR1。 PRn = Transition Matrix * PR(n - 1)。可以证明,最终的PR是收敛的。
三、Dead Ends
四、Spider traps
原文:http://www.cnblogs.com/futurehau/p/6062769.html