构建哈夫曼原理:(每个元素都是叶子结点,N 个元素共有 2N-1 个结点)
有 N 个带权值的结点,将其按以下方法构建:①②③
①选取 N 个结点集合中最小的两个权值结点构造成一个新的二叉树,且设置新结点的权值为左右孩子权值之和
②将以上选取的两个最小权值结点从原集合中删除,向集合中加入 这两个结点的跟,即 1 中创建的新结点,此时集合 元素为 N = N - 2 + 1;
③重复 ① ② 直到只剩下一个结点,该结点就是构建的二叉树的根
哈夫曼编码原理:
在哈夫曼树中,凡是左分支,即左孩子的全为 0, 凡是右分支,即右孩子的全为 1, 从根到叶子结点所组成的0 1 组合就是该叶子结点元素的编码
哈夫曼译码原理:
在哈弗曼树中,从叶子到根所组成的 0 1 组合就是所翻译得到的元素
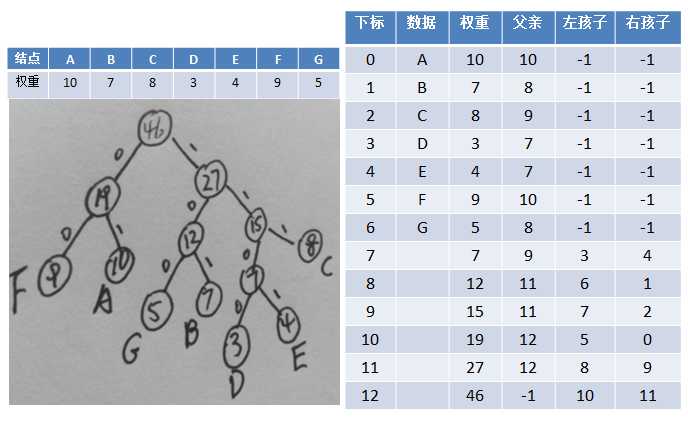
阅读代码时,可与下方图示配合,易于理解

1 void HuffmanTree::_enCode(char * Data, int * Wight, int len) { 2 // 初始化 nodes结点数组, 父、左、右全为 -1 3 int i = 0; 4 while (Data[i] != ‘\0‘) { 5 nodes[i].data = Data[i]; 6 nodes[i].weight = Wight[i]; 7 nodes[i].parent = nodes[i].lchild = nodes[i].rchild = -1; 8 i++; 9 } 10 // 创建 HuffmanTree 11 int m1, m2; // m1 存储最小值 , m2 其次 12 for (i = len; i < 2 * len - 1; ++i) { 13 _getMin(i, m1, m2); 14 nodes[i].lchild = m1; // 设置左、右 孩子 下标 15 nodes[i].rchild = m2; 16 17 nodes[i].weight = nodes[m1].weight + nodes[m2].weight; // 设置 两结点之和后的父结点权值 18 nodes[i].parent = -1; // 暂无父结点 ,置为 -1 19 nodes[m1].parent = nodes[m2].parent = i; // 设置 左、右孩子的 父结点 20 } 21 22 // 对 HuffmanTree进行编码 左结点为1 右结点为0 23 for (i = 0; i < len; ++i) { 24 int tem = nodes[i].parent; 25 int m = i; // m 作为孩子结点所在的下标,不能直接用 i,因为 i 表示的是叶子结点 26 charCode[i].ch = nodes[i].data; 27 charCode[i].length = len; 28 while (tem != -1) { // parent == -1的只有根结点, i 到 len 的都是叶子结点 29 if (nodes[tem].lchild == m) // 当前结点 nodes[i]的是父结点的左孩子 为 1 30 charCode[i].bit[--charCode[i].length] = ‘0‘; 31 else // 当前结点 nodes[i]的是父结点的右孩子 为 0 32 charCode[i].bit[--charCode[i].length] = ‘1‘; 33 m = tem; // 34 tem = nodes[tem].parent; 35 } 36 } 37 }

1 void HuffmanTree::_deCode(char * ch) { 2 int i = 0; 3 int j = 1; 4 int size = 0; 5 bool flag = true; 6 int index = 2 * nodeNumber - 2; // 下标,初始化是根所在下标 2 * nodeNumber - 2 7 while (ch[i] != ‘#‘) { // 对字符串一个个的匹配 8 // 只有当左右孩子下标为 -1 的时候表示已经到了叶子结点处,故对应了一个编码字符 9 while (nodes[index].lchild != -1 || nodes[index].rchild != -1) { 10 if (ch[i] == ‘1‘) { // 字符 1 向右 否则为1 向左 11 index = nodes[index].rchild; 12 } 13 else { 14 index = nodes[index].lchild; 15 } 16 if (ch[i] == ‘#‘) { // 为了:当用户未输入完代码时,将导致 下表 i 不能退出循环判断 ch[i]的值,故在此加上一个判断 17 data_deColde[size++] = 22; // 由于是未输入完,加入其它字符(字符十进制为22的) 提示用户含有一个未解析的代码串 18 flag = false; // 由于结束了,不再放入其它字符 flag置为 false, 而且 nodes[index].data也不是需要的字符 19 break; 20 } 21 i++; 22 } 23 if (flag == true) 24 data_deColde[size++] = nodes[index].data; // 将翻译获得的字符放入 data_deCode中 25 index = 2 * nodeNumber - 2; // 再次返回到根下标去,即从根开始继续循环执行 26 if (nodeNumber == 1) ++i; // 目的是为了: 当只编码一个 字符的时候,将不能执行 while循环而导致 i 永远为 初始值0,不能自加 27 } 28 data_deColde[size] = ‘#‘; // 作为输出结束符 29 }

1 #include <iostream> 2 using namespace std; 3 4 const int max = 8; 5 6 struct CodeNode { // 存储 编码的 0 1 字符串 7 char ch; 8 char bit[max]; 9 int length; 10 }; 11 struct HuffmanNode { // HuffmanTree 的结点数据 12 char data; 13 int parent, lchild, rchild, weight; 14 }; 15 16 class HuffmanTree { 17 public: 18 HuffmanTree(); 19 ~HuffmanTree(); 20 void _enCode(char *, int *, int); // 编码 21 void _deCode(char *); // 译码 22 void _getMin(int, int &, int &); // 返回最小的两个 下标值: 索引长度 最小值 次小值 23 void _ShowdeCode(); // 将存储在数组中的元素输出 验证 是否成功编码 24 void _getIndex(int &, int &); 25 private: 26 HuffmanNode nodes[2 * max - 1]; // 数组存储二叉树的所有结点数据 27 CodeNode charCode[max]; // 数组存储二叉树结点编码的数据 28 char data_deColde[50]; // 将翻译所得的字符放入其中 29 int nodeNumber; // 有效结点的个数 30 }; 31 32 void main() { 33 34 cout << "赫夫曼编码、译码:设置最大为 max = 8 个结点数据,最大存储译码字符为50个" << endl; 35 cout << "创建 HuffmanTree 编码:" << endl; 36 HuffmanTree HT; 37 cout << "输入待译码的 0 1字符串(100个字符,以 # 结束):"; 38 39 char ch[100]; 40 int i = 0; 41 cin >> ch[i]; 42 while (ch[i] != ‘#‘) { 43 ++i; 44 cin >> ch[i]; 45 } 46 47 HT._deCode(ch); 48 HT._ShowdeCode(); 49 50 system("pause"); 51 } 52 53 HuffmanTree::HuffmanTree() { 54 cout << "char 输入字符串结点:"; 55 char data[max]; 56 cin >> data; 57 cout << "int 输入各结点权值:"; 58 int wight[max]; 59 int i = 0; 60 while (data[i] != ‘\0‘) { 61 cin >> wight[i++]; // 注意 i++ 表示先用再加, i 最后代表着这个数组的有效元素个数 62 } 63 nodeNumber = i; 64 _enCode(data, wight, i); 65 66 } 67 HuffmanTree::~HuffmanTree() { 68 nodeNumber = 0; 69 } 70 71 void HuffmanTree::_deCode(char * ch) { 72 int i = 0; 73 int j = 1; 74 int size = 0; 75 bool flag = true; 76 int index = 2 * nodeNumber - 2; // 下标,初始化是根所在下标 2 * nodeNumber - 2 77 while (ch[i] != ‘#‘) { // 对字符串一个个的匹配 78 // 只有当左右孩子下标为 -1 的时候表示已经到了叶子结点处,故对应了一个编码字符 79 while (nodes[index].lchild != -1 || nodes[index].rchild != -1) { 80 if (ch[i] == ‘1‘) { // 字符 1 向右 否则为1 向左 81 index = nodes[index].rchild; 82 } 83 else { 84 index = nodes[index].lchild; 85 } 86 if (ch[i] == ‘#‘) { // 为了:当用户未输入完代码时,将导致 下表 i 不能退出循环判断 ch[i]的值,故在此加上一个判断 87 data_deColde[size++] = 22; // 由于是未输入完,加入其它字符(字符十进制为22的) 提示用户含有一个未解析的代码串 88 flag = false; // 由于结束了,不再放入其它字符 flag置为 false, 而且 nodes[index].data也不是需要的字符 89 break; 90 } 91 i++; 92 } 93 if (flag == true) 94 data_deColde[size++] = nodes[index].data; // 将翻译获得的字符放入 data_deCode中 95 index = 2 * nodeNumber - 2; // 再次返回到根下标去,即从根开始继续循环执行 96 if (nodeNumber == 1) ++i; // 目的是为了: 当只编码一个 字符的时候,将不能执行 while循环而导致 i 永远为 初始值0,不能自加 97 } 98 data_deColde[size] = ‘#‘; // 作为输出结束符 99 } 100 101 void HuffmanTree::_enCode(char * Data, int * Wight, int len) { 102 // 初始化 nodes结点数组, 父、左、右全为 -1 103 int i = 0; 104 while (Data[i] != ‘\0‘) { 105 nodes[i].data = Data[i]; 106 nodes[i].weight = Wight[i]; 107 nodes[i].parent = nodes[i].lchild = nodes[i].rchild = -1; 108 i++; 109 } 110 // 创建 HuffmanTree 111 int m1, m2; // m1 存储最小值 , m2 其次 112 for (i = len; i < 2 * len - 1; ++i) { 113 _getMin(i, m1, m2); 114 nodes[i].lchild = m1; // 设置左、右 孩子 下标 115 nodes[i].rchild = m2; 116 117 nodes[i].weight = nodes[m1].weight + nodes[m2].weight; // 设置 两结点之和后的父结点权值 118 nodes[i].parent = -1; // 暂无父结点 ,置为 -1 119 nodes[m1].parent = nodes[m2].parent = i; // 设置 左、右孩子的 父结点 120 } 121 122 // 对 HuffmanTree进行编码 左结点为1 右结点为0 123 for (i = 0; i < len; ++i) { 124 int tem = nodes[i].parent; 125 int m = i; // m 作为孩子结点所在的下标,不能直接用 i,因为 i 表示的是叶子结点 126 charCode[i].ch = nodes[i].data; 127 charCode[i].length = len; 128 while (tem != -1) { // parent == -1的只有根结点, i 到 len 的都是叶子结点 129 if (nodes[tem].lchild == m) // 当前结点 nodes[i]的是父结点的左孩子 为 1 130 charCode[i].bit[--charCode[i].length] = ‘0‘; 131 else // 当前结点 nodes[i]的是父结点的右孩子 为 0 132 charCode[i].bit[--charCode[i].length] = ‘1‘; 133 m = tem; // 134 tem = nodes[tem].parent; 135 } 136 // 对编码以后的代码进行输出验证: 137 cout << charCode[i].ch << ": "; 138 for (int j = charCode[i].length; j < len; ++j) { 139 cout << charCode[i].bit[j]; 140 } 141 cout << endl; 142 } 143 } 144 145 void HuffmanTree::_getMin(int len, int& m1, int& m2) { 146 bool flag = true; 147 int min1 = INT_MAX, min2 = INT_MAX, tem; 148 for (int i = 0; i < len; ++i) { 149 if (nodes[i].parent == -1 && flag) { // 保留第一位未操作的元素 150 min1 = nodes[i].weight; 151 m1 = i; 152 flag = false; 153 } 154 else if (nodes[i].parent == -1) { 155 if (nodes[i].weight < min2) { 156 min2 = nodes[i].weight; 157 m2 = i; 158 } 159 if (min2 < min1) { 160 tem = min1; 161 min1 = min2; 162 min2 = tem; 163 tem = m1; 164 m1 = m2; 165 m2 = tem; 166 } 167 } 168 169 } 170 } 171 172 void HuffmanTree::_ShowdeCode() { 173 int i = 0; 174 cout << "译码:" << endl; 175 while (data_deColde[i] != ‘#‘) { 176 cout << data_deColde[i] << " "; 177 ++i; 178 } 179 cout << endl; 180 }
原文:http://www.cnblogs.com/log-xian/p/6081888.html