数据来自 cs229 Problem Set 1 (pdf) Data: q1x.dat, q1y.dat, q2x.dat, q2y.dat PS1 Solution (pdf)
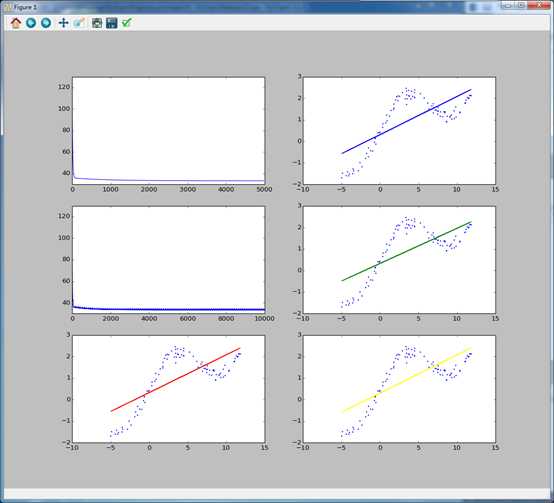
从左上往右下
batchGradientDescent的cost随迭代次数的增加而下降,和收敛结果
stochasticGradientDescent的cost随迭代次数的增加而下降,和收敛结果
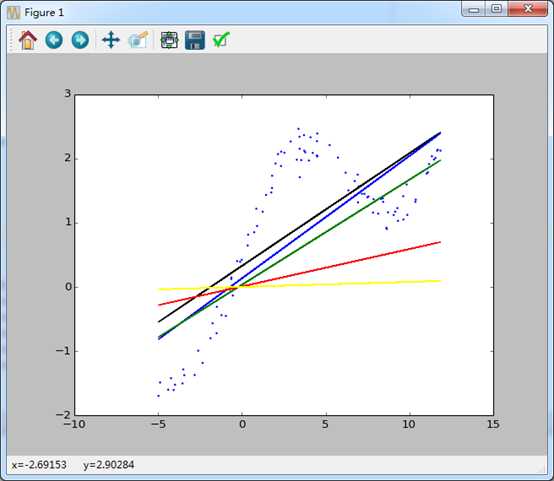
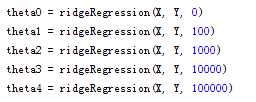
normalEquations结果,ridgeRegression结果
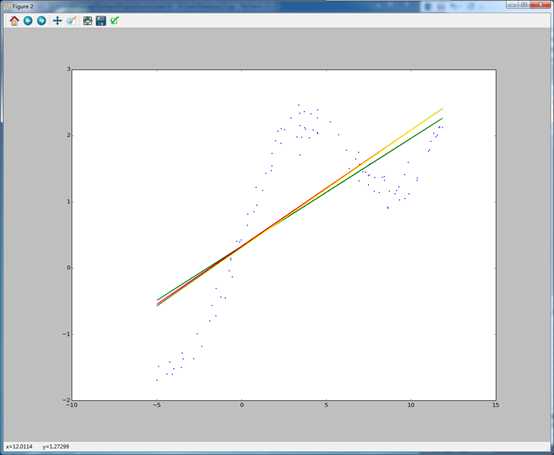
全家福,效果几乎一样
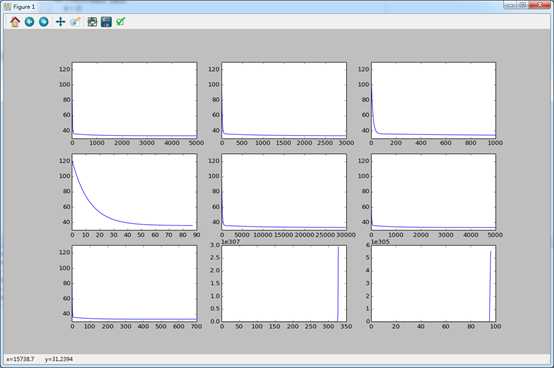
从左上往右下
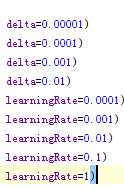
最后两张略喜感,不要笑,我初始用的是1。。。花了很长时间debug
学习速率太大后果很严重
为了全部矩阵化,花了不少时间
Matplotlib中文有问题,需要研究一下
不能这样表示theta -= learningRate * partialDerivativeFunc(theta, X, Y)
1 # !/usr/bin/python 2 # -*- coding: utf-8 -*- 3 # noooop 4 5 import numpy as np 6 import matplotlib.pyplot as plt 7 8 def batchGradientDescent(theta, X, Y, costFunc, partialDerivativeFunc, delta=0.00001, maxIterations=100000, learningRate=0.001): 9 cost = [costFunc(theta, X, Y), ] 10 for i in xrange(maxIterations): 11 theta = theta - learningRate * partialDerivativeFunc(theta, X, Y) 12 cost.append(costFunc(theta, X, Y)) 13 if abs(cost[-1] - cost[-2]) < delta: break 14 15 return theta, cost 16 17 def stochasticGradientDescent(theta, X, Y,costFunc, partialDerivativeFunc, maxIterations=100, learningRate=0.001): 18 m = len(Y) 19 cost = [costFunc(theta, X, Y), ] 20 for i in xrange(maxIterations): 21 for j in xrange(m): 22 theta = theta - learningRate *partialDerivativeFunc(theta, X[j], Y[j]) 23 cost.append(costFunc(theta, X, Y)) 24 return theta, cost 25 26 def normalEquations(X, Y): 27 return np.linalg.pinv(X.T.dot(X)).dot(X.T).dot(Y) 28 29 def ridgeRegression(X, Y, lamda = 5): 30 return np.linalg.pinv(X.T.dot(X) + lamda * np.eye(2)).dot(X.T).dot(Y) 31 32 33 34 def linearRegressionHypothesis(theta, X): 35 return theta.dot(X.T).T 36 37 38 def linearRegressionCostFunc(theta, X, Y): 39 return 0.5 * np.sum(np.array(linearRegressionHypothesis(theta, X) - Y) ** 2) 40 41 def linearRegressionPartialDerivativeFunc(theta, X, Y): 42 return (X.T.dot(linearRegressionHypothesis(theta, X) - Y) / len(Y)).T 43 44 def loadData(xdata, ydata): 45 X = [] 46 Y = [] 47 data = open(xdata) 48 for line in data.readlines(): 49 X.append((1, float(line.strip()))) 50 data = open(ydata) 51 for line in data.readlines(): 52 Y.append(float(line.strip())) 53 return np.mat(X), np.mat(Y).T 54 55 if __name__ == "__main__": 56 X, Y = loadData(‘q2x.dat‘, ‘q2y.dat‘) 57 58 theta0, cost0 = batchGradientDescent(np.array([[0, 0]]), X, Y, linearRegressionCostFunc, linearRegressionPartialDerivativeFunc) 59 theta1, cost1 = stochasticGradientDescent(np.array([[0, 0]]), X, Y, linearRegressionCostFunc, linearRegressionPartialDerivativeFunc) 60 61 theta2 = normalEquations(X, Y) 62 theta3 = ridgeRegression(X, Y) 63 64 65 f1 = plt.figure(1) 66 #f1 67 68 plt.subplot(321) 69 plt.plot(range(len(cost0)), cost0) 70 plt.subplot(322) 71 plt.scatter(np.array(X[:,1]),np.array(Y),color=‘blue‘,s=5,edgecolor=‘none‘) 72 plt.plot(np.array(X[:,1]),theta0[0,0] + theta0[0,1] * np.array(X[:,1]),color=‘blue‘) 73 74 plt.subplot(323) 75 plt.plot(range(len(cost1)), cost1) 76 plt.subplot(324) 77 plt.scatter(np.array(X[:,1]),np.array(Y),color=‘blue‘,s=5,edgecolor=‘none‘) 78 plt.plot(np.array(X[:,1]),theta1[0,0] + theta1[0,1] * np.array(X[:,1]),color=‘green‘) 79 80 plt.subplot(325) 81 plt.scatter(np.array(X[:,1]),np.array(Y),color=‘blue‘,s=5,edgecolor=‘none‘) 82 plt.plot(np.array(X[:,1]),float(theta2[0]) + float(theta2[1]) * np.array(X[:,1]),color=‘red‘) 83 84 plt.subplot(326) 85 plt.scatter(np.array(X[:,1]),np.array(Y),color=‘blue‘,s=5,edgecolor=‘none‘) 86 plt.plot(np.array(X[:,1]),float(theta3[0]) + float(theta3[1]) * np.array(X[:,1]),color=‘yellow‘) 87 88 f2 = plt.figure(2) 89 plt.scatter(np.array(X[:,1]),np.array(Y),color=‘blue‘,s=5,edgecolor=‘none‘) 90 plot1 = plt.plot(np.array(X[:,1]),theta0[0,0] + theta0[0,1] * np.array(X[:,1]),color=‘blue‘) 91 plot2 = plt.plot(np.array(X[:,1]),theta1[0,0] + theta1[0,1] * np.array(X[:,1]),color=‘green‘) 92 plot3 = plt.plot(np.array(X[:,1]),float(theta2[0]) + float(theta2[1]) * np.array(X[:,1]),color=‘red‘) 93 plot4 = plt.plot(np.array(X[:,1]),float(theta3[0]) + float(theta3[1]) * np.array(X[:,1]),color=‘yellow‘) 94 95 plt.show()
Machine learning with python - Linear Regression,布布扣,bubuko.com
Machine learning with python - Linear Regression
原文:http://www.cnblogs.com/noooop/p/3734472.html