在某块平面土地上有N个点,你可以选择其中的任意四个点,将这片土地围起来,当然,你希望这四个点围成
的多边形面积最大。
在某块平面土地上有N个点,你可以选择其中的任意四个点,将这片土地围起来,当然,你希望这四个点围成
的多边形面积最大。
第1行一个正整数N,接下来N行,每行2个数x,y,表示该点的横坐标和纵坐标。
最大的多边形面积,答案精确到小数点后3位。
数据范围 n<=2000, |x|,|y|<=100000
Solution
显然的,我们枚举对角线,我们现在的问题是找离对角线最远的点是哪两个点
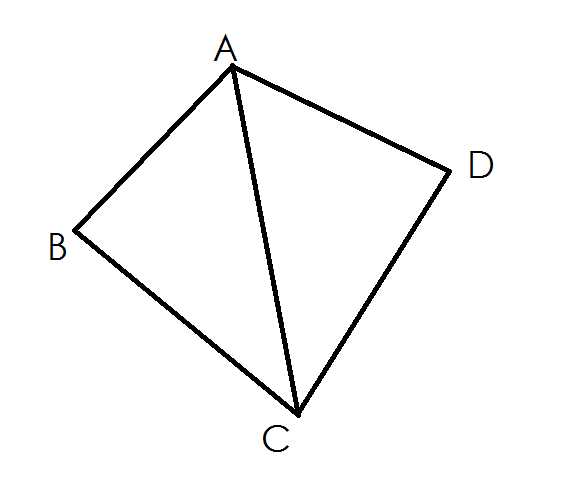
于是我们发现,当A固定,C变为逆时针的下一个点的时候,
B,D也一定是单调逆时针变动的
这里运用旋转卡壳的思想
所以这题本质是旋转卡壳,只是更加简单了
#include<stdio.h> #include<stdlib.h> #include<iostream> #include<string> #include<string.h> #include<algorithm> #include<math.h> #include<queue> #include<map> #include<vector> #include<set> #define il inline #define re register using namespace std; typedef double db; const int N=3001; const db eps=1e-8; struct P{db x,y;} a[N],s[N]; int n,top;db ans=0; il P operator-(P a,P b){ return (P){a.x-b.x,a.y-b.y}; } il db operator*(P a,P b){ return a.x*b.y-a.y*b.x; } il db S(P a,P b,P c){ return fabs((a-b)*(a-c))/2; } il db dis(P a){ return a.x*a.x+a.y*a.y; } il db cmp(P x,P y){ return (x-a[1])*(y-a[1])>0; } il void print(P a){ printf("(%lf,%lf)\n",a.x,a.y); } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%lf%lf",&a[i].x,&a[i].y); } for(int i=1;i<=n;i++) if(a[i].y<a[1].y||(a[i].y==a[1].y&&a[i].x<a[1].x)) swap(a[1],a[i]); sort(a+2,a+n+1,cmp); s[1]=a[1];s[2]=a[2];top=2; for(int i=3;i<=n;i++){ while(top>1&&(a[i]-s[top-1])*(s[top]-s[top-1])>=0) top--; s[++top]=a[i]; } if(top==4){ ans=S(s[1],s[2],s[3])+S(s[1],s[3],s[4]); printf("%.3lf",ans); return 0; } // for(int i=1;i<=top;i++) print(s[i]); for(int i=0;i<top;i++) s[i]=s[i+1]; n=top; for(int i=0;i<n;i++){ for(int j=(i+1)%n,k=(i+2)%n,l=(i+3)%n;k!=(i-2+n)%n;k=(k+1)%n){ while(S(s[i],s[j],s[k])<S(s[i],s[(j+1)%n],s[k])) j=(j+1)%n; while(S(s[i],s[l],s[k])<S(s[i],s[(l+1)%n],s[k])) l=(l+1)%n; // cout<<i<<" "<<j<<" "<<k<<" "<<l<<endl; ans=max(S(s[i],s[j],s[k])+S(s[i],s[k],s[l]),ans); } } printf("%.3lf",ans); return 0; }
原文:http://www.cnblogs.com/ExiledPoet/p/6087265.html