本文本来是想放在Borsuk-Ulam定理的应用这篇文章当中。但是这个文章实在是太长,导致有喧宾夺主之嫌,从而独立出为一篇文章,仅供参考。

(图1:Kneser叙述他的猜想原文手稿)
1. Lyusternik-Shnirel‘man定理与Greene定理
这个猜想的证明主要使用了Lyusternik与Shnirel‘man版本的Borsuk-Ulam定理,它的具体表述如下:
引理2(Lyusternik-Shnirel‘man)
令
F 为闭集,且其覆盖住1
,F
2
,?,F
n+1
S ,那么存在n
F 包含对径点(即i
x,?x∈F )。i
证明:令映射n
→R
n
1
),dist(x,F
2
),?,dist(x,F
n
))
n
n
i
=0
i
i
i
=0
n+1
但是只是用闭集不能满足我们的要求,我们还需要球用开或闭集覆盖:
推论3(开集的LS定理)
令
F 为开集,且其覆盖住1
,F
2
,?,F
n+1
S ,那么存在n
F 包含对径点。i
证明:我们只需要寻找到一个闭集族i
}
i
?F
i
i
}
n
i
n
i
ˉ
ˉ
ˉ
ˉ
ˉ
ˉ
ˉ
?F
i
n
x∈S
n
i
i
?F
i
推论4(Greene)
令
F 为开集或闭集且覆盖1
,F
2
?,F
n+1
S ,那么存在n
F 包含对径点i
证明:不妨设1
,F
2
,?,F
k
i
)
?
i
1
)
?
,?,(F
k
)
?
,F
k+1
,?,F
n+1
i
,?x
i
n
i
2. Kneser猜想与Greene的证明
下面我们介绍一下Kneser图n,k
k
)
′
′
=?
5,2
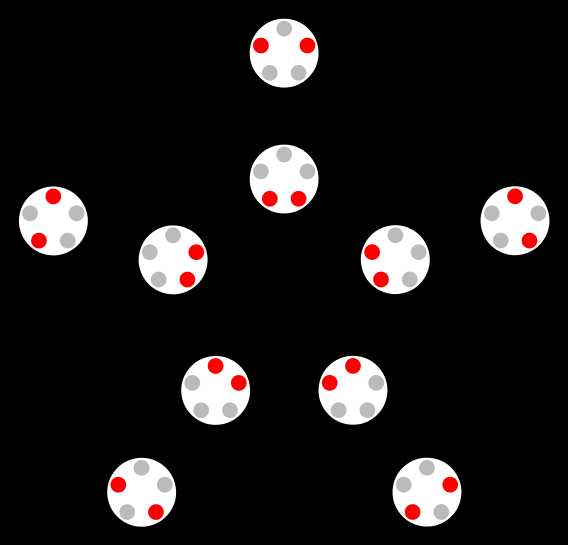
(图2:5,2
1955年,Kneser提出了如下猜想:
猜想5(Kneser)
对于任意
k>0 以及n≥2k?1 ,我们有χ(KG ,其中n,k
)=n?2k+2
χ 为染色数。
首先我们可以注意到上界是简单的。我们只需要定义染色k
)→{1,2,?,n?2k+2}
但是对于下界的证明并不是显然的。1953年Lovász首次得到了这个猜想的证明。Lovász用到了大量的代数拓扑工具,比较复杂。而在2003年,还是本科生的Greene发现了其中的组合本质,因此得到了如今广为人知的简单证明。它因为这个美妙的证明而拿了当年的Morgan奖。
证明:考虑n,k
d
k
)
d
那么假设我们有对于n,k
1
,A
2
,?A
d
?S
d
i
d
k
)
显然有i
d+1
i
′
d+1
但是对于这种情况,我们有d
?(H(x)∪H(?x))
3. Lovász的证明大意
这里我会大致写下Lovász证明到底说了什么。这个证明是现代拓扑组合学的开端。他的原始证明比较长,这里就提一下梗概:
Step 1:构造
每一个图都有对应的邻域单纯形。而领域单纯形的定义是有公共邻居的节点集合组成的单纯形。比如说这样的图:
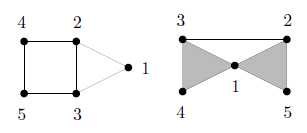
(图3:左图是原图
我们可见,集合
Step 2:
我们可见上图是
由于图的m+2
m+2
m+2
)
m+2
)
m+2
)
n+1
→S
m
Step 3: 验证n,k
)
Lovász的证明是用拓扑对组合问题进行研究的开端。而这篇文章体现了Borsuk-Ulam定理在拓扑组合这一新兴学科中的重要应用,并激励了一大批人对拓扑组合问题进行研究,对于这一方法应用的历史沿革将附在最后(来自Longueville)。
4. Bárány的证明与Schrijver定理
其实Greene并不是第一个对Lovász的证明进行改进的人。早在1978年,Bárány就给出了一个较为简单的证明,但是它利用了Gale 引理。该引理叙述如下:
引理6(Gale)
对于任意
d≥0 以及任意k≥1 ,存在包含2k+d 个点的集合X?S ,使得任意d
S 的开半球必包含d
k 个X 中的点。
(图4:一种开半球的分划)
对于该引理的证明我们略去,但是这个引理能够给出Kneser猜想的证明。
证明:对于d
i
d
k
)
i
i
我们可见Bárány的证明虽然利用了Gale引理,但是它同样可以用在其他一些集合上。比如说Schrijver图。有如下定义:
定义7(Schrijver)
定义一个集合
S?[n] 是2? 稳定(2? stable)的,如果k∈S ,那么对于?l∈S ,2≤|l?k|≤n?2 。而定义Schrijver图SG(n,k) 为所有稳定的集合S 给出的Kneser图。
显然我们可以发现,?
n?2k+2
引理8(Ziegler加强的Gale引理)
对于任意
d≥0 以及任意k≥1 ,存在包含2k+d 个点的集合X?S ,使得任意d
S 的开半球必包含d
k 个X 中的点。且这k 个点的集合是2? 稳定的。
这个引理的证明可见Matou?ek书上的76页。而有了这个引理,Bárány的证明可以很简单地就应用到Schrijver图上,且证明完全相同。
5. Dol‘nikov定理与超图上的Kneser猜想
从上面的Schrijver图我们可以看出,实际上我们可以对任何超图定义它的Kneser图,也即对于超图1
,F
2
∈F
1
∩F
2
=?
定义9(超图的
2? 染色)我们称超图
H=(X,F) 是2? 可染色的如果存在映射X→{1,2} (1,2 看成点的颜色),使得任意一个超边都包含两种颜色的点。
同时,我们可以定义"缺损
定义10(缺损
2? 染色数)
cd 2
(H)=min{|Y|:(X?Y,{F∈F:F∩Y=?)是2?可染色的}}
也就是超图
H 至少去掉多少点(以及与这个点相连的超边)能够使它变成2? 可染色的超图。
而这样的Kneser图有个比较好的性质。
引理11(图
G 的Kneser超图实现)任意一个图
G ,都存在一个超图H ,使得KG(H)=G 。
证明:取图的补图,然后定义为补图上的边编号,将补图上的编号赋予节点即可。如下是一个例子
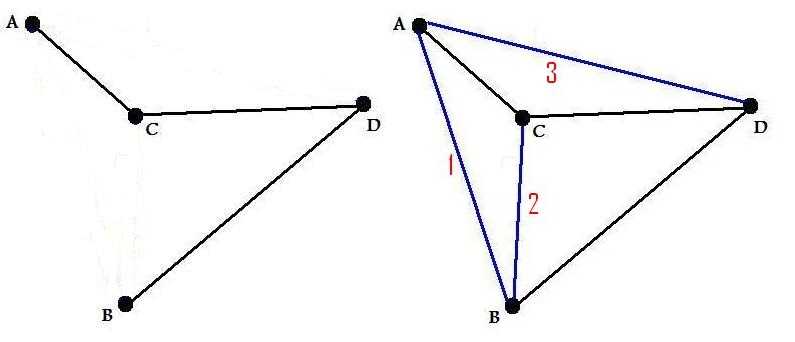
(图5:
那么通过对Kneser图的观察(这里的Kneser图看成k
)
2
(F)=n?2k+2
因此我们通过观察就有了如下的结论:
定理12(Dol‘nikov)
对于任意有限的超图
H=(X,F) ,我们有χ(KG(H))≥cd 2
(F)
证明:证明使用到的就是类似Greene的方法。令d
i
i
d+1
=S
d
?(A
1
∪?∪A
d
)
由于Greene定理,对于某i
注记:通过引理11,我们就知道,任意一个图我们都能够通过这样的方法找到它染色的一个下界!
对于一些特殊的超图,我们是否有更一般的结论呢?对于前面我们定义超图的
同样,对于Kneser图,我们也可以推广到Kneser超图。
定义13(Kneser超图)
KG 是超图,其中r
(n,k)=(X,F)
X=([n] ,而超边的集合k
)
F 中为r 个互不相交的x∈X 组成。
从这里可以看出,我们原来定义的Kneser图2
(n,k)
猜想14(Erd?s的Kneser染色猜想)
χ(KG r
(n,k))=?n?(k?1)r
r?1
?
该猜想已由Alon, Frankl和Lovász在1986年证明成立。他们的证明主要也用了代数拓扑的结论。而同理,我们也可以定义Schrijver图的推广。我们可以定义集合r
(n,k)
s?stab
猜想15 (Alon-Drewnowski-?uczak)
χ(KG r
(n,k)
s?stab
)=?n?(k?1)r
r?1
?
这个猜想现在还是一个开放问题。Ziegler首次证明了r
(n,k)
r?stab
)
r
(n,k))
r
(n,k)
~
r?stab
)
r
(n,k)
~
r?stab
6. Matou?ek的组合证明以及推广
Matou?ek在2000年也给出了用Tucker引理的证明与一个纯组合的证明。这个证明的思想被迅速推广到上面很多定理的证明当中,从而从众多拓扑证明中脱颖而出,有令人耳目一新之感。如下是他证明的主要思想:
首先注意到Tucker引理可以有如下推广:
引理16(八面体Tucker引理——Octahedral Tucker‘s lemma)
对于任意集合
A,B∈[n] ,且A∩B=? ,A∪B≠? ,对于任意满足λ(A,B)=?λ(B,A) ,且值域是{+1,?1,+2,?2,?,+(n?1),?(n?1)} 的函数λ 。存在两个集合组(A 以及1
,B
1
)
(A ,满足2
,B
2
)
(A ,且有1
,B
1
)?(A
2
,B
2
)
λ(A 。1
,B
1
)=?λ(A
2
,B
2
)
其中
(A 的意思是,1
,B
1
)?(A
2
,B
2
)
A 且1
?B
1
A ,且至少一个是真包含。2
?B
2
这个引理的证明同样略去,具体可见Matou?ek文章。而用此引理,Kneser猜想的证明就变得比较简单了。
定理5 (Matou?ek)Kneser猜想是正确的。(PS:标记为5是因为Kneser猜想在本文中标为5)
证明:假设k
)→{1,2,?,t}
其中
若1
,B
1
)?(A
2
,B
2
)
1
,B
1
)+λ(A
2
,B
2
)
2
|+|B
2
|≤2k?2
1
|+|B
1
||<|A
2
|+|B
2
|
1
,B
1
)+λ(A
2
,B
2
)=0
2
|+|B
2
|>2k?2
但是如果1
|+|B
1
|≤2k?2
1
|+|B
1
|
1
|+|B
1
|>2k?2
但是通过第二种情况可以发现,存在1
,S
2
这个证明是否巧妙地用Tucker引理给出了一个Kneser猜想的证明,主要就是用Tucker构造出了两个相邻但是染色一样的点。当然,上面所展现的并不是Matou?ek原文,而是利用原文类似的想法由Meunier给出的。用这样类似的证明,Ziegler在2004年首次给出了Schrijver定理的组合证明,但是证明中使用了有向拟阵(Oriented Matroid),而且这个证明较长。所以Meunier类似于前面的方法给出了Schrijver定理简短的证明。
定义17(交错长
alt )对于
A,B?[n] ,定义alt(A,B) 为最长的单调增的数列x ,使得1
,x
2
,?,x
l
x ,且i
∈A∪B
x 则i
∈A
x ;i+1
∈B
x 则i
∈B
x 。i+1
∈A
比如说
有了这一个工具,我们就可以得出以下的Schrijver定理:
定理18(Schrijver)
Schrijver图染色数是
n?2k+2
证明:假设k
)→{1,2,?,t}
情况与上面类似,
类似地,如果1
,B
1
)?(A
2
,B
2
)
1
,S
2
2
,B
2
)≤2k?1
2
,B
2
)+alt(A
1
,B
1
)≠0
1
,x
2
,?,x
l
2
,B
2
)
1
∈A
2
2
1
1
,B
1
)
2
,B
2
)
1
,B
1
)
1
1
1
2
,B
2
)
2
2
2
,B
2
)>2k?1
1
,B
1
)>2k?1
我们类似地可以证明Dol‘nikov定理,以下的证明来自Ziegler:
定理12(Dol‘nikov)
对于任意有限的超图
H=(X,F) ,我们有χ(KG(H))≥cd 2
(F)
证明:类似地,假设2
(F)>t
显然这样的映射满足八面体Tucker引理的条件。同时通过类似的说明(这里就不再耗费时间讲述了)可以构造出1
,S
2
Matou?ek的组合证明又提出了一个新的思路:通过拓广Tucker引理以及构造合适的函数(利用反证法给出的条件可以说明要满足值域在r
(n,k)
~
r?stab
)
p
?
7.拓扑组合的历史注记
以下基本来自于Longueville对于Kneser猜想所著的文章“25 years proof of the Kneser conjecture”
(1)拓扑的应用
在前面提到过,在组合中使用拓扑工具来源于Lovász对于Borsuk-Ulam定理纯熟的应用。也许Borsuk-Ulam定理最好的一个推广来自于Albrecht Dold在1983年的定理:
定理19(Dold)
令
G 为非平凡的有限群,自由作用在(形态较好的)空间X 与Y 上。假如X 是n?1 -连通,且Y 的维数是m ,那么如果存在G? 等价的映射,那么m≥n 。这里G? 等价意思是,?g∈G ,f(g?x)=g?f(x)
如果将n
m
随着时代的发展,代数拓扑中的工具基本都在组合中找到了它们自己的位置。从同调到上同调,示性类到谱序列,都有了组合上的应用,比如Dmitry Kozlov所著的"图同态的复形"。甚至微分拓扑同样有在组合中的对应,比如Robin Forman提出的"离散Morse理论"。
对于这些方法的应用有很多。最引人注目的就是“图染色问题”。现在很多图和超图的染色数都有了界的估计,而估计这些界的方法用的就是拓扑工具。各种“划分问题”同样被解决了,而最著名的即“项链问题”,又Noga
Alon在1987年解决。更多地,复杂度问题,比如说线性决策树算法的复杂度,以及与Aanderaa–Karp–Rosenberg猜想相关的单调图性质的复杂度,同样可以用拓扑组合进行解决。另外一个很大的理论及“偏序集的拓扑”。在1980年瑞典数学家Anders
Bj?rner提出了偏序集的shellability这一概念。如果我们有一个偏序集,我们就可以给出一个单纯形,从而定义一个拓扑空间。Bj?rner提出的偏序集的shellability也即,这一个相关的拓扑空间是一族球。这个组合的概念以及拓扑的结果给出了许多的应用,比如说Bruhat序以及代数组合中的一个问题。同时值得注意的是,如果用了shellability,我们很容易证明n,k
)
(2)回归组合
虽然许多组合定理能够被拓扑证明,一个自然的问题是,这些拓扑定理是否能够证明组合问题?2000年组合学又一次突破,即Matou?ek首次给出了Kneser猜想的组合证明,也就是我们前面所提到的。证明中用的Tucker引理与Borsuk-Ulam定理是等价的。同样,Borsuk-Ulam定理的组合兄弟们也能够用来解决“平均划分问题”。同时,离散数学中许多具体的证明需要快速计算同调群或其他不变量,而这些快速的程序都依赖于组合的构造。
代数拓扑来自于组合拓扑的研究,正如Lefschetz首次在杜克大学提出代数拓扑时所说的一样:
“The assertion is often made of late that all mathematics is composed of algebra and topology. It is not so widely realized that the two subjects interpenetrate so that we have an algebraic topology as well as a topological algebra”
——Solomen Lefschetz
而最后一句话对于现在的组合与拓扑来说同样成立。
8.鸣谢与拓展阅读
最后,感谢吳耀琨老师所上的“计算拓扑”课,没有这门课程,我是不会注意到Hatcher书上小小的一个Borsuk-Ulam定理居然能用这门有用的应用,能够成为组合领域的一大利器。
同时感谢网上的各位学者,将他们的美妙的成果放在了网络之上,让我有能力一窥这一领域的浩瀚博大。这里我给出我这篇文章所参考的资料:
[1]Some Mathematics Of Theoretical Computer Science:很简要地给出了Greene的证明,是我第1,2部分的来源
[2]25 years proof of the Kneser conjecture :给出了Kneser猜想的历史,是第3,7部分的主要来源
[3]Kneser‘s Conjecture and its Generalizations :伊朗人写的presentation,是我4,5部分的主要来源
[4]Combinatorial topology and the coloring of Kneser graphs:法国人的presentation,是我第6部分的来源
这一领域还有许多可以引用的文献,这里我就不一一列举了,从我这几篇文献的引用就可以大致了解了。
原文:http://www.cnblogs.com/misaka01034/p/KneserConjecture.html