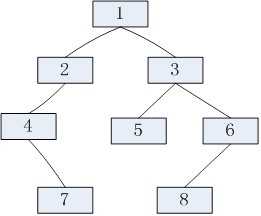
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并输出它的后序遍历序列。
输入可能包含多个测试样例,对于每个测试案例,
输入的第一行为一个整数n(1<=n<=1000):代表二叉树的节点个数。
输入的第二行包括n个整数(其中每个元素a的范围为(1<=a<=1000)):代表二叉树的前序遍历序列。
输入的第三行包括n个整数(其中每个元素a的范围为(1<=a<=1000)):代表二叉树的中序遍历序列。
对应每个测试案例,输出一行:
如果题目中所给的前序和中序遍历序列能构成一棵二叉树,则输出n个整数,代表二叉树的后序遍历序列,每个元素后面都有空格。
如果题目中所给的前序和中序遍历序列不能构成一棵二叉树,则输出”No”。
8 1 2 4 7 3 5 6 8 4 7 2 1 5 3 8 6 8 1 2 4 7 3 5 6 8 4 1 2 7 5 3 8 6
7 4 2 5 8 6 3 1 No
#include <stdio.h> #include <stdlib.h> #include <memory.h> int findRoot(int *arr1,int begin1,int end1,int *arr2,int begin2,int end2,int *final); int final[1000]; int flag = 999; int main(void){ int n,i; int arr1[1000]; int arr2[1000]; while(scanf("%d",&n) != EOF && n <= 1000 && n >= 1){ //initialize memset(arr1,0,sizeof(int)*1000); memset(arr2,0,sizeof(int)*1000); memset(final,0,sizeof(int)*1000); flag = 999; //input for(i=0;i<n;i++) scanf("%d",&arr1[i]); for(i=0;i<n;i++) scanf("%d",&arr2[i]); if(findRoot(arr1,0,n-1,arr2,0,n-1,final) == 0) printf("No\n"); else{ for(i=flag+1;i<1000;i++) printf("%d ",final[i]); printf("\n"); } } return 0; } int findRoot(int *arr1,int begin1,int end1,int *arr2,int begin2,int end2,int *final){ int i,j; int sum = 0; if(begin1==end1 && begin2 == end2){ final[flag] = arr1[begin1]; flag--; return 1; } for(i=begin1 ; i<=end1;i++){ for(j=begin2 ; j <=end2 ; j++){ if(arr1[i] == arr2[j]) sum++; } } if(sum != (end1-begin1+1) && sum != (end2 - begin2+1)){ return 0; } final[flag] = arr1[begin1]; flag--; int numberofRoot = -1; for(i=begin2 ; i<=end2 ; i++){ if(arr1[begin1] == arr2[i]){ numberofRoot = i; //printf("找到跟在arr2的坐标为%d\n",numberofRoot); break; } } if(numberofRoot != end2){ //printf("right %d %d %d %d\n",begin1+numberofRoot-begin2+1,end1,numberofRoot+1,end2); if(!findRoot(arr1,begin1+numberofRoot-begin2+1,end1,arr2,numberofRoot+1,end2,final)){ return 0; } } if(numberofRoot != begin2){ //printf("left %d %d %d %d\n",begin1+1,begin1+numberofRoot-begin2,begin2,numberofRoot-1); if(!findRoot(arr1,begin1+1,begin1+numberofRoot-begin2,arr2,begin2,numberofRoot-1,final)){//左子树 return 0; } } return 1; }
剑指OFFER之重建二叉树(九度OJ1385),布布扣,bubuko.com
原文:http://www.cnblogs.com/xing901022/p/3737599.html