注:fjutoj基本每周都有一次周赛,欢迎大家都来参加!
网址:http://210.34.193.66:8080/vj/index.jsp
A题:来源 POJ 2773
题意:给两个数m和k,问第k 个和m 互素的数是多少(从1到无穷大)。
思路:
二分 + 容斥
先求出m 的素因子p[],数x 和m 互素就意味着x 不存在p 数组中的任意一个素因子,现在要 求n 下面不存在p[]素因子的数的数量可以转化为,n-存在p[]中任意一个素因子的数的个数(经典题型,用容斥可以求),现在二分(k,INF)可以求出答案。

1 #include<stdio.h> 2 #define N 1000010 3 #define LL long long 4 const LL INF = 0x7fffffffffffffff; 5 bool pri[N]; 6 int prim[N], po=0; 7 void Init() 8 { 9 for(int i=2;i<N;i++) 10 { 11 if(!pri[i]) prim[po++]=i; 12 for(int j=0;j<po&&(LL)i*prim[j]<N;j++) 13 { 14 pri[i*prim[j]]=1; 15 if(i%prim[j]==0) break; 16 } 17 } 18 } 19 20 int data[30], co; 21 22 void fun(int x) 23 { 24 int i=0; 25 co=0; 26 while(i<po && (LL)prim[i]*prim[i]<=x) 27 { 28 bool c=0; 29 while(x%prim[i]==0) 30 { 31 c=1; 32 x/=prim[i]; 33 } 34 if(c) data[co++]=prim[i]; 35 i++; 36 } 37 if(x!=1) data[co++]=x; 38 } 39 40 void dfs(int limit, int j, LL y, LL now, LL &all) 41 { 42 if(limit==0) 43 { 44 all += y/now; 45 return ; 46 } 47 for(int i=j; i<co; i++) 48 { 49 dfs(limit-1, i+1, y, now*data[i], all); 50 } 51 } 52 LL solve(LL x) 53 { 54 LL sum=x, flag=-1; 55 for(int i=1; i<=co; i++) 56 { 57 LL all=0; 58 dfs(i, 0, x, 1, all); 59 sum+=flag*all; 60 flag *= -1; 61 } 62 return sum; 63 } 64 65 LL er(LL l, LL r, LL x) 66 { 67 while(l<r) 68 { 69 LL mid = (l+r)/2; 70 if(solve(mid)>=x) r=mid; 71 else l=mid+1; 72 } 73 return l; 74 } 75 76 int main() 77 { 78 Init(); 79 int x,y; 80 while(~scanf("%d%d",&x, &y)) 81 { 82 fun(x); 83 printf("%lld\n", er(y, INF, y)); 84 } 85 return 0; 86 }
B题:来源 HDU 1730
题意:
思路:
博弈
很容易产生的错误判断:如果两个子相邻,那么这个的胜者是后手,如果不相邻,胜者是先手,那么判断先手胜利的行数,最后如果是奇数则先手胜,偶数则后手胜(我因此WA了两次...)。举个错误样例: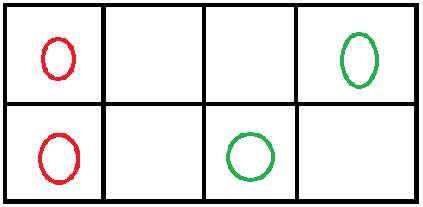 ,如果按上面思路,两行都是先手胜,那么应该是后手赢,但先手其实可以将第一行的红点移动一格,这样先手就赢了。
,如果按上面思路,两行都是先手胜,那么应该是后手赢,但先手其实可以将第一行的红点移动一格,这样先手就赢了。
事实上,这里应该是nim博弈的模型,首先,我们可以判断出一点,双方的棋子只会不断接近(如果一人后退一步,另一人可以跟进一步,保持局面不变)。接着,既然两者只能接近,那么就可以看作是n 堆,每一堆x个,每个玩家每轮可以拿走一个、两个、...直至拿完。接下来就不解释了。

1 #include<stdio.h> 2 int max(int a, int b) { return a>b?a:b; } 3 int main() 4 { 5 int n, m, x, y; 6 while(~scanf("%d%d",&n, &m)) 7 { 8 int ans = 0; 9 for(int i=0; i<n; i++) 10 { 11 scanf("%d%d",&x, &y); 12 if(x+1==y || x==y+1); 13 else ans ^= ( max(x, y) - (x+y-max(x, y)) - 1); 14 } 15 if(ans) printf("I WIN!\n"); 16 else printf("BAD LUCK!\n"); 17 } 18 return 0; 19 }
C题:来源 POJ 3671
题意:
思路:
用两个数组a[]、b[],a[i]表示i前面2的个数,b[i]表示i后面1的个数(遍历两遍可以求出a、b数组),如果以i 为中心(1、2转折点),要修改的数个数为a[i-1]+b[i+1],遍历一遍求出最小值即可。

1 #include<stdio.h> 2 #define N 30010 3 int a[N], b[N], c[N]; 4 int main() 5 { 6 int n; 7 while(~scanf("%d",&n)) 8 { 9 a[0]=0; 10 for(int i=1; i<=n; i++) 11 { 12 scanf("%d", &c[i]); 13 if(c[i]==1) a[i]=a[i-1]; 14 else a[i]=a[i-1]+1; 15 } 16 b[n+1]=0; 17 for(int i=n; i>0 ;i--) 18 { 19 if(c[i]==1) b[i]=b[i+1]+1; 20 else b[i]=b[i+1]; 21 } 22 int mint = N; 23 for(int i=1; i<=n; i++) 24 { 25 if(a[i-1]+b[i+1]<mint) mint = a[i-1]+b[i+1]; 26 } 27 printf("%d\n", mint); 28 } 29 return 0; 30 }
D题:来源 POJ 3663
题意:
思路:
排序 + 二分
对数组排序后,遍历一遍,s-a[i]就是分界点,二分出小于等于他的第一个数,比他小的都满足条件。

1 #include<stdio.h> 2 #include<string.h> 3 #include<algorithm> 4 using namespace std; 5 6 int a[20005]; 7 int er(int l, int r, int x) 8 { 9 while(l<r) 10 { 11 int mid = (l+r)/2; 12 if(a[mid]<=x) l=mid+1; 13 else r=mid; 14 } 15 return l; 16 } 17 18 int main() 19 { 20 int n, m; 21 while(~scanf("%d%d",&n,&m)) 22 { 23 for(int i=0; i<n; i++) 24 scanf("%d", &a[i]); 25 sort(a, a+n); 26 int ans = 0; 27 for(int i=n-1; i>0; i--) 28 { 29 int x = m-a[i]; 30 int num = er(0, i, x) - 0; 31 ans += num; 32 } 33 printf("%d\n", ans); 34 } 35 return 0; 36 }
E题:来源 POJ 1028
题意:
思路:
随手写个栈模拟一下就好了。

1 #include<stack> 2 #include<string> 3 #include<iostream> 4 using namespace std; 5 6 string st[200]; 7 int top=0; 8 int mt=0; 9 10 void push(string s) 11 { 12 st[++top]=s; mt=top; 13 } 14 15 void pop() 16 { 17 if(top==0) cout<<"Ignored"<<endl; 18 else cout<<st[--top]<<endl; 19 } 20 21 int main() 22 { 23 st[top]="http://www.acm.org/"; 24 string s; 25 while(cin>>s) 26 { 27 if(s[0]==‘Q‘) break; 28 if(s[0]==‘V‘) 29 { 30 cin>>s; cout<<s<<endl; 31 push(s); 32 } 33 else if(s[0]==‘B‘) pop(); 34 else if(top==mt) cout<<"Ignored"<<endl; 35 else cout<<st[++top]<<endl; 36 } 37 return 0; 38 }
原文:http://www.cnblogs.com/hchlqlz-oj-mrj/p/6188252.html