计数排序
计数排序假设n个输入元素中的每一个都是0到k区间内的一个整数,其中k为某个整数。当
k=O(n)时,排序的运行时间为@(n)
计数排序的基本思想是: 对每一个输入元素x,确定小于x的元素个数。利用这个信息,就可以直接把x
放到它在输出数组中的位置上了。 例如,如果有17个元素小于x,则x就应该在第18个输出位置上。当有
几个元素相同时,这一方案要略作修改。因为不能把它们放在同一个输出位置上。
在计数排序算法的代码中,假设输入是一个数组A[1...n], A.length=n. 我们还需要两个数组,B[1..n]
存放排序的输出,C[0...k]提供临时存储空间。
COUTING-SORT(A,B,k)
let C[0...k] be a new array
for i=0 to k
C[i] = 0
for j=1 to A.length
C[A[j]] = C[A[j]] +1
//C[i] now contains the number of elements equal to i.
for i=1 to k
C[i] = C[i] + C[i-1]
//C[i] now contains the number of elements less than or equal to i
for j=A.length downto l
B[C[A[j]]] = A[j]
C[A[j]] = C[A[j]] - 1
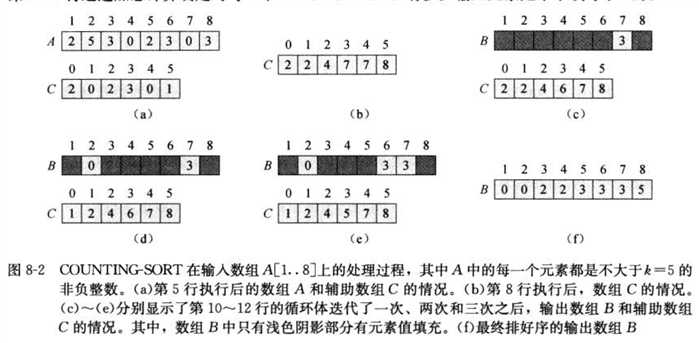
计数排序@(n)
计数排序的一个重要性在就是稳定,具有相同值的元素在输出数组中的相对次序与他们在输入数组中的相对次序相同。
原文:http://www.cnblogs.com/zhoug2020/p/6189084.html