一、问题描述
某售货员要到若干城市去推销商品,已知各城市之间的路程(或旅费)。他要选定一条从驻地出发,经过每个城市一次,最后回到驻地的路线,使总的路程(或总旅费)最小。
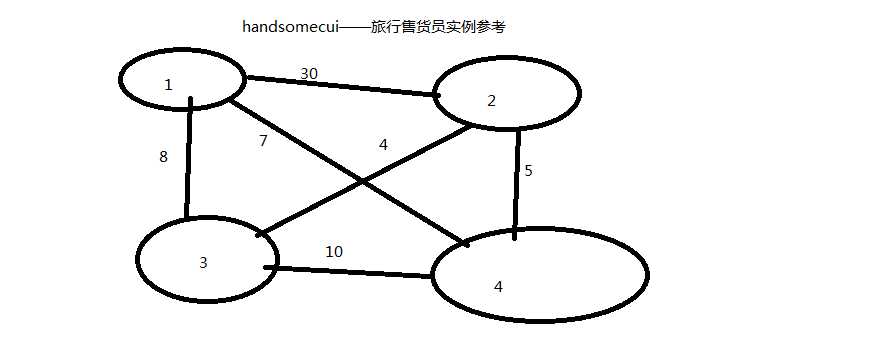
如下图:1,2,3,4 四个城市及其路线费用图,任意两个城市之间不一定都有路可达。
二、问题理解
1.分支限界法利用的是广度优先搜索和最优值策略。
2.利用二维数组保存图信息a[MAX_SIZE][MAX_SIZE]
其中a[i][j]的值代表的是城市i与城市j之间的路径费用
一旦一个城市没有通向另外城市的路,则不可能有回路,不用再找下去了
下面是书上介绍的一种方法,书里面有一些错误,经过修改可以得出正确答案了;具体通过代码分析:
package essay; import java.util.PriorityQueue; public class BBTSP { public static float [][]a; private static class MinHeap extends PriorityQueue<HeapNode>{ public MinHeap() { super(); } public void put(HeapNode node) { add(node); } public HeapNode removeMin() { HeapNode poll = poll(); return poll; } } private static class HeapNode implements Comparable{ float lcost, //子树费用下界 cc, //当前费用 rcost; //x[s:n-1]中定点最小出边费用和 int s; //相当于计数器,表示在当前解答树的第几层; int[] x; public HeapNode(float lc, float ccc, float rc, int ss, int[] xx) { lcost = lc; cc = ccc; rcost = rc; s = ss; x = xx; } @Override public int compareTo(Object x) { float xlc = ((HeapNode)x).lcost; if(lcost < xlc)return -1; if(lcost == xlc)return 0; return 1; } } public static float bbTsp(int v[]){ int n = v.length - 1; MinHeap heap = new MinHeap(); float[] minOut = new float[n + 1]; float minSum = 0; for(int i = 1; i <= n; i++){ float min = Float.MAX_VALUE; for(int j = 1; j <=n; j++){ if(a[i][j] < min){ min = a[i][j]; } } if(min == Float.MAX_VALUE) return Float.MAX_VALUE; minOut[i] = min; minSum += min; } int[] x = new int[n]; int[] minx = new int[n]; for(int i = 0; i < n; i++)x[i] = i+1; HeapNode enode = new HeapNode(0, 0, minSum, 0, x); float bestc = Float.MAX_VALUE; while(enode != null && enode.s < n - 1){ x = enode.x; if(enode.s == n - 2){ if(a[x[n - 2]][x[n - 1]] < Float.MAX_VALUE && a[x[n - 1]][1] < Float.MAX_VALUE && enode.cc + a[x[n - 2]][x[n - 1]] + a[x[n - 1]][1] < bestc ){ bestc = enode.cc + a[x[n - 2]][x[n - 1]] + a[x[n - 1]][1]; enode.cc = bestc; enode.lcost = bestc; //System.out.println(x[0]+","+x[1]+","+x[2]+","+x[3]); enode.s++; minx = x; heap.put(enode); } } else{ for(int i = enode.s + 1; i < n; i++){ if(a[x[enode.s]][x[i]] < Float.MAX_VALUE){ float cc = enode.cc + a[x[enode.s]][x[i]]; float rcost = enode.rcost - minOut[x[enode.s]]; float b = cc + rcost; //更新当前费用,最小出边费用和,子树费用下界; //子树费用下界,也就是当前最小的可能解 if(b < bestc){ int[] xx = new int[n]; for(int j = 0; j < n; j++)xx[j] = x[j]; xx[enode.s + 1] = x[i]; xx[i] = x[enode.s + 1]; //访问到i节点,将i节点与enode.s+1节点交换位置复制给xx; HeapNode node = new HeapNode(b, cc, rcost, enode.s+1, xx); heap.put(node); } } } } enode = (HeapNode)heap.removeMin(); } for(int i = 0; i < n; i++){ v[i + 1] = minx[i]; } return bestc; } }
先介绍这个BBTSP类:
BBTSP的构成:
1.类MinHeap继承了priority_queue也就是我们要放入的优先队列;
2.类HeapNode这个是我们自定义的一个数据结构,放在优先队列中;
3.bbTsp是本问题的解决类
4.a是邻接矩阵,作为我们要解决问题的图;
解决问题的思想:
用最小堆表示活结点优先队列,最小堆中最小元素是HeapNode,中的lcost作为子树费用下界,cc为当前费用,rcost是剩余点的最小出边费用和,s记录当前在解答树的第几层,x数组存储最优解;广度优先遍历,子树费用下界作为最小堆的排列依据,每次取到enode(当前最优解)for循环儿子结点,得到最优可行子树儿子解,结点插入最小堆;当遍历到最后一个结点的时候,比较得到最小回到1城市的最优解;注意最优解要单独存放在minx数组中,课本上写的有些问题;
测试代码:
package essay; import org.junit.*; public class MyTest { @Test public void test() { BBTSP bbtsp = new BBTSP(); bbtsp.a = new float[5][5]; bbtsp.a[1][1] = 0; bbtsp.a[1][2] = 30; bbtsp.a[1][3] = 8; bbtsp.a[1][4] = 7; bbtsp.a[2][1] = 30; bbtsp.a[2][2] = 0; bbtsp.a[2][3] = 4; bbtsp.a[2][4] = 5; bbtsp.a[3][1] = 8; bbtsp.a[3][2] = 4; bbtsp.a[3][3] = 0; bbtsp.a[3][4] = 10; bbtsp.a[4][1] = 7; bbtsp.a[4][2] = 5; bbtsp.a[4][3] = 10; bbtsp.a[4][4] = 0; int[] v = new int[5]; System.out.println("最小费用是:" + bbtsp.bbTsp(v)); System.out.println("路径是: "); for(int i = 1; i <= 4; i++){ System.out.printf("%d-->", v[i]); } System.out.println(1); } }
来源:http://www.cnblogs.com/handsomecui
欢迎访问:handsomecui.top
原文:http://www.cnblogs.com/handsomecui/p/6214937.html