本文主要是根据MC随机抽样思想,进行已知分布的抽样,对于数据分析有用,主要做如下几个版本
(1)数据部分,概率密度分布
const double energy[210]={21.000000, 22.000000, 23.000000, 24.000000, 25.000000, 26.000000, 27.000000, 28.000000, 29.000000, 30.000000, 31.000000, 32.000000, 33.000000, 34.000000, 35.000000, 36.000000, 37.000000, 38.000000, 39.000000, 40.000000, 41.000000, 42.000000, 43.000000, 44.000000, 45.000000, 46.000000, 47.000000, 48.000000, 49.000000, 50.000000, 51.000000, 52.000000, 53.000000, 54.000000, 55.000000, 56.000000, 57.000000, 58.000000, 59.000000, 60.000000}; const double probability[210]={ 0.003172, 0.001603, 0.003484, 0.000000, 0.000365, 0.003666, 0.001642, 0.005879, 0.005202, 0.022721, 0.027685, 0.056204, 0.075032, 0.118366, 0.163304, 0.215736, 0.283005, 0.343148, 0.422711, 0.494946, 0.574868, 0.652534, 0.717833, 0.794975, 0.842019, 0.909445, 0.924232, 0.986227, 0.974940, 1.000000, 0.964995, 0.968823, 0.896359, 0.866523, 0.761573, 0.687310, 0.557857, 0.420584, 0.248464, 0.038391};
(2)归一化概率密度分布并积分得到分布函数
for (int x = 1; x < 210; x++) { sump += probability[x]; } pp[0] = probability[0]; for (int x = 1; x < 210; x++) { pp[x] = pp[x - 1] + probability[x]; }
(3)抽样函数
1 double IncidentGammaEnergy() 2 { 3 double rand=G4UniformRand(); 4 double sum=pp[0]; 5 double pre_sum=0.; 6 int p_size = sizeof(probability)/sizeof(probability[0]); 7 for(int k=0;k<p_size-1;k++) 8 { 9 if ((rand>pre_sum) && (rand<=sum)) 10 { 11 return energy[k]+(energy[k+1]-energy[k])*(rand-pre_sum)*(sum-pre_sum); 12 } 13 pre_sum = sum; 14 sum=pp[k+1]; 15 } 16 return energy[p_size-1]; 17 }
clear clc
% data name is cs137.mat,it has sub var x and y load cs137 x=x; y=y; % normalize y=y/sum(y); n=length(x); % fenbuhanshu pp=zeros(n,1); for i=1:n-1 pp(i+1)=pp(i)+y(i+1); end % sample now pre_sum=0; sumup=pp(1); m=100000; rand_number=rand(m,1); out=zeros(m,1); for j=1:m for i=1:n-1 if(rand_number(j)>pre_sum)&&(rand_number(j)<=sumup) out(j)=x(i); end pre_sum=sumup; sumup=pp(i+1); end out=out‘; end % plot and compare [histvalue,nbins]=hist(out,1:1:n); histvalue=histvalue‘; plot(nbins,histvalue/sum(histvalue)) hold on plot(x,y,‘r‘) hold off legend(‘抽样结果‘,‘原始数据‘)
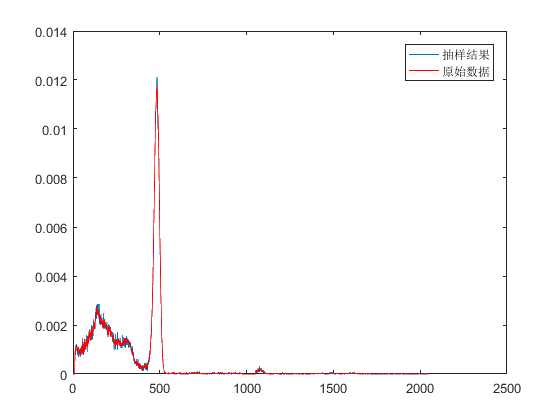
抽样100000次(m=100000)结果为
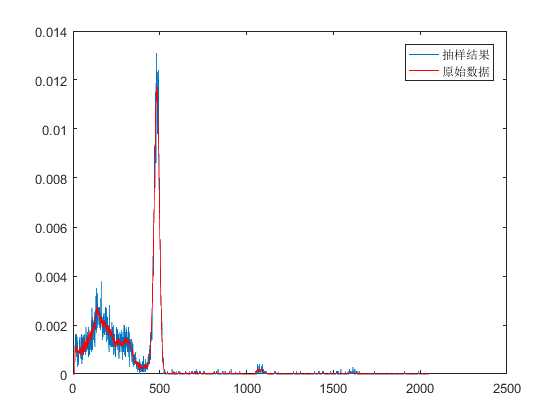
m=10000
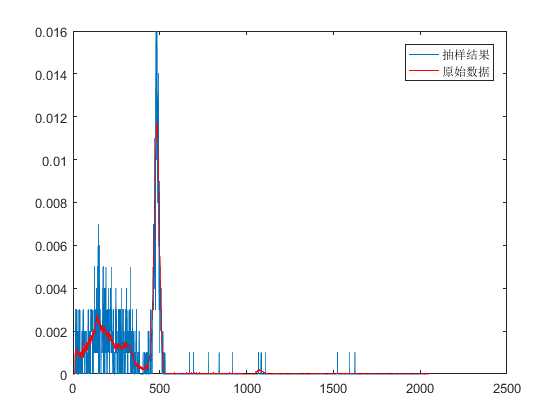
m=1000;
C#实现
参考文献:
1、许淑艳老师的《蒙特卡罗方法在实验核物理中的应用》的第三章《由已知分布的随机抽样》
原文:http://www.cnblogs.com/liq07lzucn/p/6231043.html