欧拉函数证明
欧拉函数定义:定义一个数n,φ(n)为不大于n的,与n互质的数的个数。
证明方法用到容斥定理:容斥定理的原理如图:
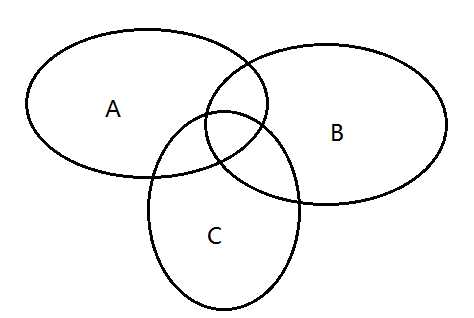
A∪B∪C=A+B+C - A∩B - B∩C - A∩C + A∩B∩C;
欧拉函数证明:
小于等于n的基数有n个,讨论所有n的素因子,只要是素因子的倍数的是都不是n的互质数。
首先如果如果n为素数那么,φ(n)=n-1;
如果n不是素数,只要除去n的因子和n的因子的倍数就可以了,①因为任意一个数都能表示成若干个素数的乘积,所以只要出去质因子的以及倍数就够可以了,因为如果出去的不是质因子,那么这个因子还能继续被分解成若干个质因子的乘积又能被n整除,综上那么就有基数n减去所有是质因子倍数的个数,然后加上任意两个,减三个,加四个…质因子积的倍数(容斥定理),②φ(n)=n-n/p1-n/p2-n/p3-n/p4….-n/pn+n/(p1*p2)+n/(p1*p3)…(容斥定理),所以②式得出的就是所有的互质数的个数。可化简为φ(n)=n*(1-1/p1) *(1-1/p2) *(1-1/p3)…*(1-1/pk);
①式证明:当n=2时,显然成立;
假设当n=k时成立;
那么当n=k+1时,如果n是素数那么显然成立,如果不是素数那么n一定能分解成两个数的乘积,又因为n=k时是成立的,所有综上所述结论成立
另外欧拉函数还有两条重要的性质,可以快速求出欧拉函数的值(a为N的质因素)
若( N%a ==0&&(N/a)%a ==0)则有:E(N)= E(N/a)*a;
若( N%a ==0&&(N/a)%a !=0)则有:E(N)= E(N/a)*(a-1);
原文:http://www.cnblogs.com/wuwangchuxin0924/p/6233211.html