In the previous section we saw how to use vectors to solve geometry problems.
Now we are going to learn how to use some basic linear algebra to do line
intersection, and then apply line intersection to a couple of other problems.
Line-Line Intersection
One of
the most common tasks you will find in geometry problems is line intersection.
Despite the fact that it is so common, a lot of coders still have trouble with
it. The first question is, what form are we given our lines in, and what form
would we like them in? Ideally, each of our lines will be in the form
Ax+By=C, where A, B and C are the numbers which define the line.
However, we are rarely given lines in this format, but we can easily generate
such an equation from two points. Say we are given two different points,
(x1, y1) and (x2, y2), and want to
find A, B and C for the equation above. We can do so by setting
A =
y2-y1
B = x1-x2
C =
A*x1+B*y1
Regardless of how the lines are
specified, you should be able to generate two different points along the line,
and then generate A, B and C. Now, lets say that you have lines, given by the
equations:
A1x + B1y =
C1
A2x + B2y = C2
To find
the point at which the two lines intersect, we simply need to solve the two
equations for the two unknowns, x and y.
double det = A1*B2 - A2*B1
if(det == 0){
//Lines are parallel
}else{
double x = (B2*C1 - B1*C2)/det
double y = (A1*C2 - A2*C1)/det
}
To see where this comes from, consider multiplying the top equation by
B2, and the bottom equation by B1. This gives you
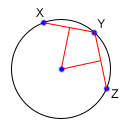
To find the perpendicular bisector of XY, find the line from X to Y, in the
form Ax+By=C. A line perpendicular to this line will be given by the
equation -Bx+Ay=D, for some D. To find D for the particular line we are
interested in, find the midpoint between X and Y by taking the midpoint of the x
and y components independently. Then, substitute those values into the equation
to find D. If we do the same thing for Y and Z, we end up with two equations for
two lines, and we can find their intersections as described above.
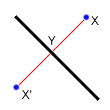
Reflection
Reflecting a point across a line requires the same techniques as finding a
circle from 3 points. First, notice that the distance from X to the line of
reflection is the same as the distance from X‘ to the line of reflection. Also
note that the line between X and X‘ is perpendicular to the line of reflection.
Now, if the line of reflection is given as Ax+By=C, then we already
know how to find a line perpendicular to it: -Bx+Ay=D. To find D, we
simply plug in the coordinates for X. Now, we can find the intersection of the
two lines at Y, and then find X‘ = Y - (X - Y).
Rotation
Rotation doesn‘t really fit in with line
intersection, but I felt that it would be good to group it with reflection. In
fact, another way to find the reflected point is to rotate the original point
180 degrees about Y.
Imagine that we want to rotate one point around
another, counterclockwise by θ degrees. For simplicity, lets assume that we are
rotating about the origin. In this case, we can find that x‘ = x Cos(θ) - y
Sin(θ) and y‘ = x Sin(θ) + y Cos(θ). If we are rotating about a
point other than the origin, we can account for this by shifting our coordinate
system so that the origin is at the point of rotation, doing the rotation with
the above formulas, and then shifting the coordinate system back to where it
started.
Convex Hull
A convex hull of a set
of points is the smallest convex polygon that contains every one of the points.
It is defined by a subset of all the points in the original set. One way to
think about a convex hull is to imagine that each of the points is a peg
sticking up out of a board. Take a rubber band and stretch it around all of the
points. The polygon formed by the rubber band is a convex hull. There are many
different algorithms that can be used to find the convex hull of a set of
points. In this article, I‘m just going to describe one of them, which is fast
enough for most purposes, but is quite slow compared to some of the other
algorithms.

First, loop through all of your points and find the leftmost point. If there is a tie, pick the highest point. You know for certain that this point will be on the convex hull, so we‘ll start with it. From here, we are going to move clockwise around the edge of the hull, picking the points on the hull, one at a time. Eventually, we will get back to the start point. In order to find the next point around the hull, we will make use of cross products. First, we will pick an unused point, and set the next point, N, to that point. Next, we will iterate through each unused points, X, and if (X-P) x (N-P) (where P is the previous point) is negative, we will set N to X. After we have iterated through each point, we will end up with the next point on the convex hull. See the diagram below for an illustration of how the algorithm works. We start with P as the leftmost point. Now, say that we have N and X as shown in the leftmost frame. In this case the cross product will be negative, so we will set N = X, and there will be no other unused points that make the cross product negative, and hence we will advance, setting P = N. Now, in the next frame, we will end up setting N = X again, since the cross product here will be negative. However, we aren‘t done yet because there is still another point that will make the cross product negative, as shown in the final frame.
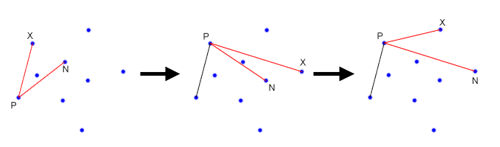
The basic idea here is that we are using the cross product to find the point which is furthest counterclockwise from our current position at P. While this may seem fairly straightforward, it becomes a little bit tricky when dealing with colinear points. If you have no colinear points on the hull, then the code is very straightforward.
convexHull(point[] X){
int N = lengthof(X);
int p = 0;
//First find the leftmost point
for(int i = 1; i<N; i++){
if(X[i] < X[p])
p = i;
}
int start = p;
do{
int n = -1;
for(int i = 0; i<N; i++){
//Don‘t go back to the same point you came from
if(i == p)continue;
//If there is no N yet, set it to i
if(n == -1)n = i;
int cross = (X[i] - X[p]) x (X[n] - X[p]);
if(cross < 0){
//As described above, set N=X
n = i;
}
}
p = n;
}while(start!=p);
}
Once we start to deal with colinear points, things get trickier. Right away we
have to change our method signature to take a boolean specifying whether to
include all of the colinear points, or only the necessary ones. //If onEdge is true, use as many points as possible for
//the convex hull, otherwise as few as possible.
convexHull(point[] X, boolean onEdge){
int N = lengthof(X);
int p = 0;
boolean[] used = new boolean[N];
//First find the leftmost point
for(int i = 1; i<N; i++){
if(X[i] < X[p])
p = i;
}
int start = p;
do{
int n = -1;
int dist = onEdge?INF:0;
for(int i = 0; i<N; i++){
//X[i] is the X in the discussion
//Don‘t go back to the same point you came from
if(i==p)continue;
//Don‘t go to a visited point
if(used[i])continue;
//If there is no N yet, set it to X
if(n == -1)n = i;
int cross = (X[i] - X[p]) x (X[n] - X[p]);
//d is the distance from P to X
int d = (X[i] - X[p]) ? (X[i] - X[p]);
if(cross < 0){
//As described above, set N=X
n = i;
dist = d;
}else if(cross == 0){
//In this case, both N and X are in the
//same direction. If onEdge is true, pick the
//closest one, otherwise pick the farthest one.
if(onEdge && d < dist){
dist = d;
n = i;
}else if(!onEdge && d > dist){
dist = d;
n = i;
}
}
}
p = n;
used[p] = true;
}while(start!=p);
}原文:http://www.cnblogs.com/xpvincent/p/3738319.html