组合数学相关

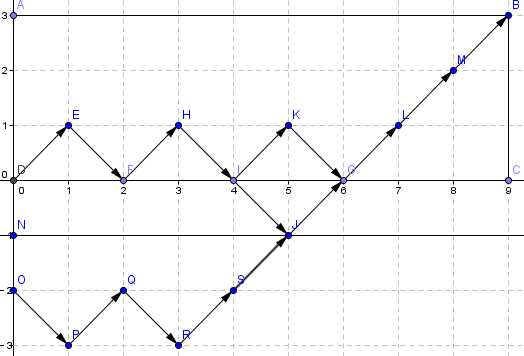
从坐标(0,x)出发，每次向右上或右下移动√2个单位，移动过程中触碰过x轴，直到移动到(z,y)，其方案集合为F1；从坐标(0,-x)出发，每次向右上或右下移动√2个单位，直到移动到(z,y)，其方案集合为F2。若x,y,z>0，则有|F1|=|F2|。

证明：对于F1中每一种走法，对其进行这样一种变换：设其与x轴第一个交点为(w,0)，将横坐标0~w的路线以x轴对称，则唯一地得到了F2中的一种方案。对于F2的一种方案，显然在F1中有且只有一种方案可以变换为成它（该变换是自己的逆变换），所以F1与F2中元素一一对应，集合大小相等。

相关问题：BZOJ1856

lxhgww最近接到了一个生成字符串的任务，任务需要他把n个1和m个0组成字符串，但是任务还要求在组成的字符串中，在任意的前k个字符中，1的个数不能少于0的个数。现在lxhgww想要知道满足要求的字符串共有多少个，聪明的程序员们，你们能帮助他吗？

题解：考虑将方案变为坐标轴中的路线，每加入一个字符即向右移动一次，加入1为右上，加入0为右下，则问题变成了：从(0,1)移动到(n+m,n-m+1)，不触碰x轴的方案数。

ANS=C(n+m,n-m)-C(n+m,m-1)

const
  mo:int64=20100403;
var
  i,j,k,l,n,m:longint;
  a:array[0..2000001]of int64;
  ans:int64;
function ksm(x,y:int64):int64;
var z:int64;
begin
  z:=1;
  while y>0 do
  begin
    if y mod 2=1 then z:=(z*x)mod mo;
    y:=y div 2; x:=(x*x)mod mo;
  end;
  exit(z);
end;
function c(x,y:int64):int64;
begin
  if x=y then exit(1);
  exit(((a[x]*ksm(a[y],mo-2))mod mo*ksm(a[x-y],mo-2))mod mo);
end;
begin
  readln(n,m);
  a[0]:=1;
  for i:=1 to n+m do a[i]:=a[i-1]*i mod mo;
  ans:=c(n+m,n-m)-c(n+m,m-1);
  ans:=(ans mod mo+mo)mod mo;
  writeln(ans);
end.

组合数学相关

原文：http://www.cnblogs.com/GhostReach/p/6253758.html