欧拉函数

void Euler_Sieve_Method(int * euler, int n) {
    euler[1] = 1;
    for (int i = 2; i < n; i++) {
        euler[i] = i;
    }
    for (int i = 2; i < n; i++) {
        if (euler[i] == i) {
            for (int j = i; j < n; j += i) {
                euler[j] = euler[j] / i * (i - 1);
            }
        }
    }
}

View Code

void Euler_Sieve_Method(int * euler, int n):计算欧拉函数1~n的函数值，保存在euler数组中。

欧拉函数的一些性质：

　　通式：

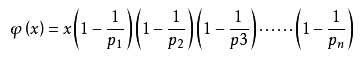
　　欧拉定理：对于互质的正整数a和n，有aφ(n) ≡ 1 mod n。

　　欧拉函数是积性函数——若m,n互质，φ(mn)=φ(m)φ(n)。

　　设a为N的质因数，若(N % a == 0 && (N / a) % a == 0) 则有E(N)=E(N / a) * a；若(N % a == 0 && (N / a) % a != 0) 则有：E(N) = E(N / a) * (a - 1)。

欧拉函数

原文：http://www.cnblogs.com/dramstadt/p/6254419.html