无题面神题
原题意:
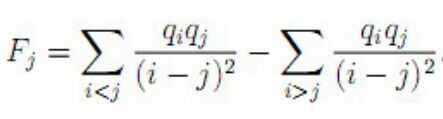
求所有的Ei=Fi/qi。
题解:
qi被除掉了,则原式中的qj可以忽略。
用a[i]表示q[i],用b[j-i]来表示±1/((j-i)^2)(j>i时为正,j<i时为负)
则求E[j]就是多项式乘法了。
因为是FFT,所以b的下标要增加到0及以上。
这题时限有30s,比某题友好多了。
代码:
type xs=record x,y:double; end; arr=array[0..1000000]of xs; var e,t:arr; a:array[1..5]of arr; n,m,i:longint; function jian(a,b:xs):xs; begin jian.x:=a.x-b.x; jian.y:=a.y-b.y; end; function jia(a,b:xs):xs; begin jia.x:=a.x+b.x; jia.y:=a.y+b.y; end; function cheng(a,b:xs):xs; begin cheng.x:=a.x*b.x-a.y*b.y; cheng.y:=a.x*b.y+a.y*b.x; end; procedure fft(xx,s,nn,mm:longint); var i,j:longint; w:xs; begin if nn=1 then begin a[xx+2,s]:=a[xx,s]; exit; end; for i:=0 to nn div 2-1 do begin t[i]:=a[xx,i*2+s]; t[i+nn div 2]:=a[xx,i*2+1+s]; end; for i:=0 to nn-1 do a[xx,s+i]:=t[i]; fft(xx,s,nn div 2,mm*2); fft(xx,s+nn div 2,nn div 2,mm*2); for i:=0 to nn div 2-1 do begin j:=s+i; w:=cheng(e[i*mm],a[xx+2,j+nn div 2]); t[j]:=jia(a[xx+2,j],w); t[j+nn div 2]:=jian(a[xx+2,j],w); end; for i:=s to s+nn-1 do a[xx+2,i]:=t[i]; end; begin read(m); for i:=0 to m-1 do read(a[1,i].x); for i:=1 to m-1 do a[2,i].x:=-1/(m-i)/(m-i); for i:=m+1 to m*2-1 do a[2,i].x:=1/(i-m)/(i-m); n:=1; while n<m*2 do n:=n*2; for i:=0 to n-1 do e[i].x:=cos(pi*2*i/n); for i:=0 to n-1 do e[i].y:=sin(pi*2*i/n); fft(1,0,n,1); fft(2,0,n,1); for i:=0 to n-1 do a[3,i]:=cheng(a[3,i],a[4,i]); for i:=0 to n-1 do e[i].y:=-e[i].y; fft(3,0,n,1); for i:=m to m*2-1 do writeln((a[5,i].x/n):0:3); end.
原文:http://www.cnblogs.com/GhostReach/p/6257602.html