5. Longest Palindromic Substring

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example:

Input: "babad"

Output: "bab"

Note: "aba" is also a valid answer.

Example:

Input: "cbbd"

Output: "bb"
写一下动态规划的思路，这个是leetcode上的动态规划思路

Approach #3 (Dynamic Programming) [Accepted]

To improve over the brute force solution, we first observe how we can avoid unnecessary re-computation while validating palindromes. Consider the case $\text{‘‘ababa‘‘‘‘ababa‘‘. If we already knew that ‘‘bab‘‘‘‘bab‘‘ is a palindrome, it is obvious that ‘‘ababa‘‘‘‘ababa‘‘ must be a palindrome since the two left and right end letters are the same.}$

We define P(i,j)P(i,j) as following:

$$\mathrm{P(i,j)=\{true,if\; the\; substring Si\dots Sj is\; a\; palindromefalse,otherwise. P(i,j)=\{true,if\; the\; substring Si\dots Sj is\; a\; palindromefalse,otherwise.}$$

Therefore,

P(i, j) = ( P(i+1, j-1) \text{ and } S_i == S_j )P(i,j)=(P(i+1,j?1) and S?i??==S?j??)

The base cases are:

P(i, i) = trueP(i,i)=true

P(i, i+1) = ( S_i == S_{i+1} )P(i,i+1)=(S?i??==S?i+1??)

This yields a straight forward DP solution, which we first initialize the one and two letters palindromes, and work our way up finding all three letters palindromes, and so on...

Complexity Analysis

• Time complexity : O(n^2)O(n?2??). This gives us a runtime complexity of O(n^2)O(n?2??).

• Space complexity : O(n^2)O(n?2??). It uses O(n^2)O(n?2??) space to store the table.

这是以abade为例，得到的dp矩阵

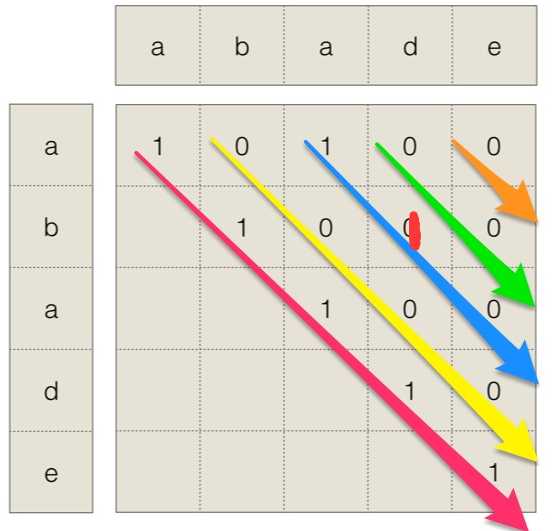
下面上代码：

    public String longestPalindrome(String s) {
        boolean[][] flag = new boolean[s.length()][s.length()];
        int maxlen = 0,start = 0;
        for(int i = 0;i < s.length(); i++){
        	flag[i][i] = true;
        	maxlen = 1;
        	start = i;
        }
        for(int i = 0;i < s.length()-1; i++)
        	if(s.charAt(i)==s.charAt(i+1)){
        		flag[i][i+1] = true;
        		maxlen = 2;
        		start = i;
        	}
        for(int len = 3; len<= s.length(); len++)
        	for(int i = 0;i < s.length()-len+1; i++){
        		int j = i+len-1;
        		if(s.charAt(i)==s.charAt(j)&&flag[i+1][j-1]==true){
        			flag[i][j] = true;
        			maxlen = len;
        			start = i;
        		}
        	}
        return s.substring(start, start+maxlen);
    }

5. Longest Palindromic Substring

原文：http://www.cnblogs.com/lxk2010012997/p/6261452.html