图像处理复习整理（2.数字频域加强）

频域图像处理

傅里叶思想：周期连续性函数能够被正弦余弦公式表示出来：

其中：

一维连续傅里变换：

反变换：

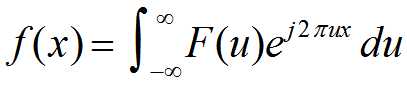
一维离散的傅里叶变换：

反变换：变过去就一定要变回来

二维离散傅里叶变换：

反变换：

由于傅里叶变换结果一般都是复数，由此可以用极坐标表示：

傅里叶谱：

相角：

能量谱：

式中，R(u,v)和I(u,v)分别是F(u,v)的实部和虚部。

F(0,0)被称为直流成分，也是频谱图之中最大的数值，很多时候都是比其他的大多个数量级。

图像的傅里叶变化是可以分为两步进行的，从某种意义上来说，验证了之前的假设，即x与y非线性相关。

傅里叶变换的性质：

1. 周期性
2. 共轭对称性

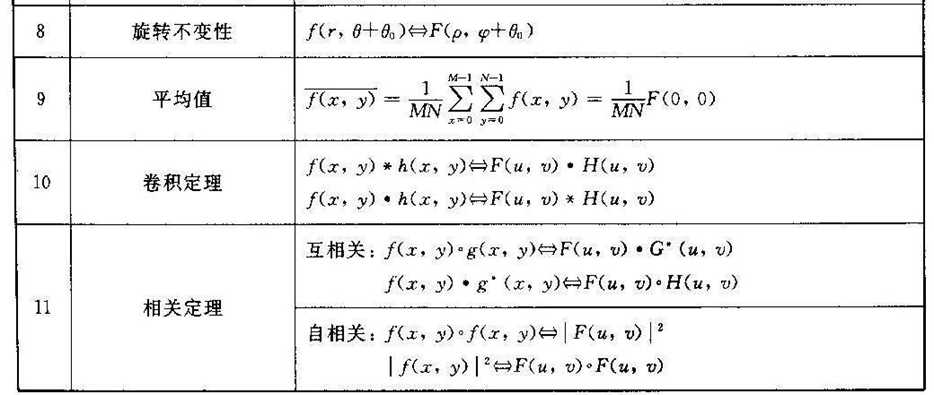
Matlab函数:

一维快速Fourier变换及反变换: fft和ifft

二维快速Fourier变换及反变换: fft2和ifft2n维快速Fourier变换及反变换: fftn和ifftn

离散Fourier变换矩阵: dftmtx，fftshift, ifftshift，angle

低通滤波器

理想低通滤波器

包含原有信息的比例

n阶巴特沃斯低通滤波器

D₀是自己需要设计的一个参考距离。

高斯低通滤波器

高通滤波器：

理想高通滤波器：

n阶巴特沃斯高通滤波器

高斯高通滤波器

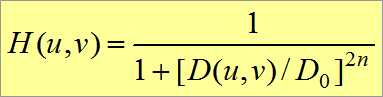
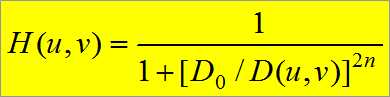
之所以理想滤波器不行的原因是，图像如果发生突变，会产生振铃现象。所以出现了巴特沃斯滤波器和高斯滤波器，而高斯滤波器是最好的。

图像处理复习整理（2.数字频域加强）

原文：http://www.cnblogs.com/kangronghu/p/6267321.html