Linear Regression和Logistic Regression都是广义线性模型的特例
当概率密度函数可以写成下面的形式,我们称属于自然指数分布族:
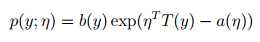
η 特性[自然]参数 natural parameter
T (y) 充分统计量 sufficient statistic 一般情况下 T (y) = y
a(η) 积累量母函数log partition function
e?a(η) 用来归一化
Bernoulli –> exponential family
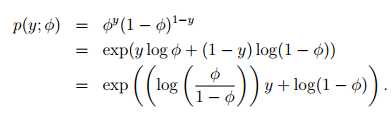
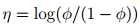
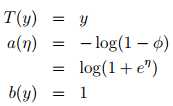
反解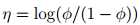 ,logistic函数是这么来的:
,logistic函数是这么来的:
φ =1/(1 + e?η)
Gaussian -> exponential family(假设σ2= 1)
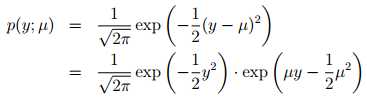
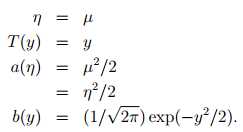
众多概率统计学过的分布都属于自然指数分布族
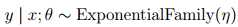
第三步可以考虑为设计策略,η是输入变量的线性组合
扯点远的
Bayesian vs Frequentist
频率学派认为θ未知的,确定的变量(上帝知道)
估计θ的方法是,θ的值应该使得观察到的样本最大可能的出现(经验风险最小化)
贝叶斯学派观点见生成学习算法
下面举几个栗子
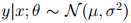
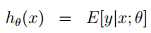 =μ
=μ根据μ = η有:
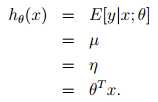
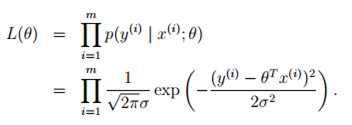
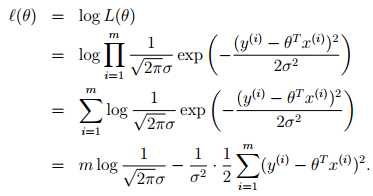
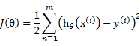
选择 最小化
最小化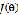
一气呵成
Logistic Regression
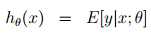 =φ
=φ根据φ =1/(1 + e?η)有:
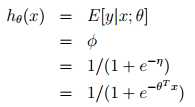
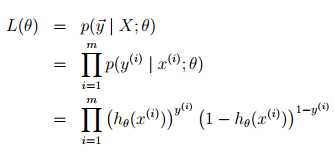
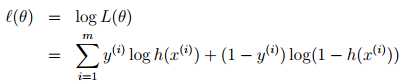
选择 最大化?(θ)
最大化?(θ)
又一气呵成
可以看出构造GLM难点在于第一步,对y|x; θ的分布建模。
如何确定y|x; θ的分布。。。。不知道。。。。
只能假定你已经y|x; θ的分布是某个指数族分布
最后一个栗子
k分类问题
y ∈{1 2, . . . , k}
一个比较合理的假设是对y|x; θ服从多项分布(multinomial distribution)
K个输出的概率记为φ1, . . . , φk,其中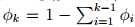
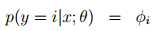
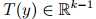 定义如下
定义如下
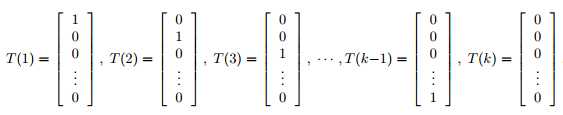
指示函数(indicator function) 1{·}
1{True} = 1, 1{False} = 0 比如 1{2 = 3} = 0
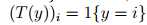
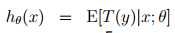
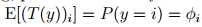
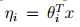
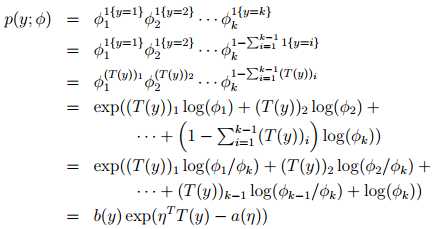
得到:
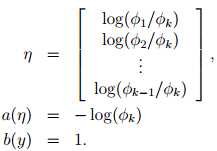
反解得:
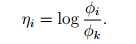
定义: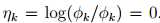
叠加得:
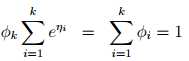
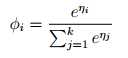
上式称为softmax 函数

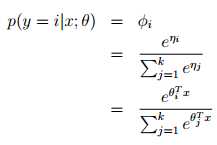
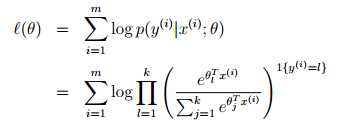
选择 最大化?(θ)
最大化?(θ)
这种处理多分类问题称为softmax regression
3. Generlized Linear Models,布布扣,bubuko.com
原文:http://www.cnblogs.com/noooop/p/3741776.html