题意:问使天平平衡需要改动的最少的叶子结点重量的个数。
分析:天平达到平衡总会有个重量,这个重量可以由某个叶子结点的重量和深度直接决定。
如下例子:
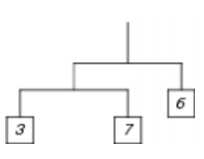
假设根结点深度为0,结点6深度为1,若以该结点为基准(该结点值不变),天平要平衡,总重量是12(6 << 1),而若以结点3为基准,天平要平衡,总重量也是12(3 << 2)。
由此可得,只需要算出以每个结点为基准的总重量,若该重量下对应的叶子结点最多,则使天平在此重量下平衡改变的叶子结点数最少。
#pragma comment(linker, "/STACK:102400000, 102400000") #include<cstdio> #include<cstring> #include<cstdlib> #include<cctype> #include<cmath> #include<iostream> #include<sstream> #include<iterator> #include<algorithm> #include<string> #include<vector> #include<set> #include<map> #include<stack> #include<deque> #include<queue> #include<list> #define Min(a, b) ((a < b) ? a : b) #define Max(a, b) ((a < b) ? b : a) typedef long long ll; typedef unsigned long long llu; const int INT_INF = 0x3f3f3f3f; const int INT_M_INF = 0x7f7f7f7f; const ll LL_INF = 0x3f3f3f3f3f3f3f3f; const ll LL_M_INF = 0x7f7f7f7f7f7f7f7f; const int dr[] = {0, 0, -1, 1, -1, -1, 1, 1}; const int dc[] = {-1, 1, 0, 0, -1, 1, -1, 1}; const int MOD = 1e9 + 7; const double pi = acos(-1.0); const double eps = 1e-8; const int MAXN = 1000000 + 10; const int MAXT = 10000 + 10; using namespace std; char s[MAXN]; map<ll, int> mp; int cnt;//叶子结点总数 void dfs(int st, int et, int deep){ if(s[st] == ‘[‘){ int tmp = 0; for(int i = st + 1; i <= et; ++i){ if(s[i] == ‘[‘) ++tmp; if(s[i] == ‘]‘) --tmp; if(!tmp && s[i] == ‘,‘){ dfs(st + 1, i - 1, deep + 1); dfs(i + 1, et - 1, deep + 1); } } } else{ ++cnt; ll sum = 0; for(int i = st; i <= et; ++i){ sum = sum * 10 + s[i] - ‘0‘; } ++mp[sum << deep]; } } int main(){ int T; scanf("%d", &T); while(T--){ mp.clear(); cnt = 0; scanf("%s", s); int len = strlen(s); dfs(0, len - 1, 0); int ans = 0; for(map<long long, int>::iterator it = mp.begin(); it != mp.end(); ++it){ ans = Max(ans, (*it).second); } printf("%d\n", cnt - ans); } return 0; }
UVA - 12166 Equilibrium Mobile (修改天平)(dfs字符串表示的二叉树)
原文:http://www.cnblogs.com/tyty-Somnuspoppy/p/6284174.html