线性表是一种线性结构,由n(n >= 0)个类型相同的数据元素a0,..., an-1组成的有限序列。记为:
LinearList = (a0, a1,..., an-1)
其中n为线性表元素的个数,称为线性表长度。如果n = 0,LinearList为空表;如果n > 0, ai(0 < i < n-1)有且只有一个前驱ai-1和一个后继ai+1 。a0没有前驱,an-1没有后继。关于前驱和后继,可以理解为元素在线性表中的前一个元素和后一个元素。
关于线性表的操作,一般有获取线性表的元素值,插入值,删除等等。下面是一个关于线性表的接口,表示线性表的抽象数据类型:
1 package inter; 2 3 /** 4 * 线性表的抽象数据类型 5 */ 6 public interface LList<T> { 7 /** 8 * 判断线性表是否为空 9 * @return 10 */ 11 boolean isEmpty(); 12 13 /** 14 * 获取线性表的长度 15 * @return 16 */ 17 int length(); 18 19 /** 20 * 返回线性表指定位置的元素 21 * @param i 22 * @return 如果i在线性表的范围之外,返回null 23 */ 24 T get(int i); 25 26 /** 27 * 在线性表指定位置插入元素。如果该位置已有元素,则覆盖 28 * @param i 29 * @param x 30 */ 31 void set(int i, T x); 32 33 /** 34 * 在线性表末尾添加元素 35 * @param x 36 */ 37 void append(T x); 38 39 /** 40 * 删除第i个元素并返回被删除的元素 41 * @param i 42 * @return 元素不存在,返回null 43 */ 44 T remove(int i); 45 46 /** 47 * 清空线性表 48 */ 49 void removeAll(); 50 51 /** 52 * 查找,返回首次出现的关键字为key的元素 53 * @param key 54 * @return 55 */ 56 T search(T key); 57 }
我们使用两种方式来实现线性表的接口,分别为顺序存储和链式存储。
线性表的顺序存储是用一组连续的内存单元来存储元素,也就是说ai和ai+1在内存中的位置是相邻的。这种存储结构的线性表也称为顺序表。如图:

从中可以看出,计算一个元素的存储地址只需要常量时间。因此,存取任何一个数据元素的时间复杂度是O(1),也就是说顺序表是一个随机存储结构。
顺序表的实现相对来说还是比较简单的,这里直接给出代码。
package impl; import inter.LList; /** * 线性表的顺序表示和实现 */ public class SeqList<T> implements LList<T> { private T[] elements; // 对象数组,用以记录线性表的元素 private int length; // 顺序表长度,用以记录实际元素个数 public SeqList() { this(32); } public SeqList(int size) { this.elements = (T[])new Object[size]; this.length = 0; } @Override public boolean isEmpty() { return length == 0; } @Override public int length() { return length; } @Override public T get(int i) { if (i < 0 || i > length) { return null; } return elements[i]; } @Override public void set(int i, T x) { if (x == null || i < 0 || i > length) { return; } elements[i] = x; } @Override public void append(T x) { insert(length, x); } /** * 在指定位置插入元素 * @param i * @param x */ public void insert(int i, T x) { if (x == null) return; // 下标容错 i = i < 0 ? 0 : (i > length ? length : i); // 扩充容量 if (length == elements.length) { T[] temp = elements; elements = (T[])new Object[temp.length * 2]; for (int j = 0, size = temp.length; j < size; j++) { elements[j] = temp[j]; } } // 元素后移 for (int j = length - 1; j > i - 1; j--) { elements[j + 1] = elements[j]; } // 插入元素 elements[i] = x; length++; } @Override public T remove(int i) { if (i < 0 || i > length) return null; T old = elements[i]; // 元素前移 for (int j = i; j < length - 1; j++) { elements[j] = elements[j + 1]; } // 避免对象游离 elements[length - 1] = null; length--; return old; } @Override public void removeAll() { length = 0; } @Override public T search(T key) { return null; } public String toString() { StringBuffer sb = new StringBuffer(); sb.append("("); for (int i = 0; i < length;) { sb.append(elements[i].toString()); if (elements[++i] != null) { sb.append(","); } } sb.append(")"); return sb.toString(); } }
这里我们新增了一个insert方法,用于在顺序表的指定位置来插入元素。仔细查看代码,会发现一个问题。当连续插入元素时(比如1万个),而后又删除元素,可以发现elements的长度会一直维持在1万,如果之后顺序表的长度一直很小,其实这样就造成了很大的空间浪费。一个改进的建议是当删除元素时,我们主动去判断现有元素的长度是否超过容量的四分之一,否则的话将elements的长度缩减一半。
顺序表的get和set操作的时间复杂度是O(1)。插入与删除操作的主要耗时在于元素的移动。假设线性表的长度为n,在位置i插入元素的概率为pi,则插入一个元素的平均移动次数为:
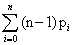
如果插入每个位置的概率相等,那么p = 1/(n + 1)
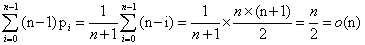
也就是说,在等概率的情况下,插入一个元素与删除一个元素的时间复杂度为O(n)。
线性表的链式存储是用若干地址分散的存储单元来存储数据元素。也就是说,在逻辑上相邻的元素在存储上不一定相邻,所以就需要采用额外的信息来记录数据元素之间的顺序关系。存储一个数据元素需要两部分:数据域和地址域。

数据域存储的是元素结点的数据,地址域存储的是下一个结点数据的地址信息。如果只有一个地址域,则称为单链表;如果有两个地址域,则称为双链表,如下图:

结点类Node。因为最终我们是将这个类作为单链表类的内部类,所以这里添加了一个private。
/** * 结点类 * 一个数据域和一个地址域 */ private class Node<E> { E data; Node<E> next; Node(E data, Node<E> next) { this.data = data; this.next = next; } Node() { this(null, null); } }
头结点的意义
单链表的头结点是一个空结点(数据域为null)。如果没有头结点,我们的删除和插入操作要分两种情况:空表插入/头部插入和中间插入/尾插入。而添加了头结点,我们可以使得这些操作的实现一致。以下是完整的代码:
package impl; import inter.LList; import java.util.Collection; /** * 线性表的链式表示和实现 * 单链表 */ public class SinglyLinkedList<T> implements LList<T> { private Node<T> head; // 头结点 /** * 默认构造器 * 构造空表 */ public SinglyLinkedList() { this.head = new Node<T>(); } @Override public boolean isEmpty() { return head.next == null; } @Override public int length() { int i = 0; Node<T> node = head.next; while (node != null) { i++; node = node.next; } return i; } @Override public T get(int i) { if (i >= 0) { Node<T> node = head; for (int j = 0; j <= i && node.next != null; j++) { node = node.next; } if (node != null) { return node.data; } } return null; } @Override public void set(int i, T x) { if (i < 0 || x == null) return; Node<T> node = head; for (int j = 0; j <= i && node.next != null; j++) { node = node.next; } if (node != null) { node.data = x; } } /** * 实现链表的插入操作。不需要移动元素,只需要遍历寻找,时间复杂度为O(n) * @param i * @param x */ public void insert(int i, T x) { if (x == null) return; // 定位到i - 1位置的元素 Node<T> node = head; for (int j = 0; j < i && node.next != null; j++) { node = node.next; } node.next = new Node<T>(x, node.next); } @Override public void append(T x) { insert(Integer.MAX_VALUE, x); } @Override public T remove(int i) { if (i >= 0) { // 定位到i - 1位置的元素 Node<T> node = head; for (int j = 0; j < i && node.next != null; j++) { node = node.next; } if (node.next != null) { T old = node.next.data; node.next = node.next.next; return old; } } return null; } @Override public void removeAll() { head.next = null; } @Override public T search(T key) { return null; } public String toString() { StringBuffer sb = new StringBuffer(); sb.append("("); Node<T> node = head.next; while (node != null) { sb.append(node.data.toString()); node = node.next; if (node != null) { sb.append(","); } } sb.append(")"); return sb.toString(); } /** * 结点类 * 一个数据域和一个地址域 */ private class Node<E> { E data; Node<E> next; Node(E data, Node<E> next) { this.data = data; this.next = next; } Node() { this(null, null); } } }
双链表的实现与此类似。有兴趣的请查看一下Java中LinkedList的实现。
原文:http://www.cnblogs.com/fellow2014/p/3735164.html