数据结构看书笔记（六）--树

　　树：
 　　树（Tree）是n(n>=0)个结点的有限集。n=0时称为空树，在任意一颗非空树中：

　　（1）有且只有一个特定的称之为根（Root）的结点；

　　（2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、……、Tm,其中每一个集合本身又是一棵树，并且称为根的子树(SubTree).
对于树的定义还要强调两点：
　　 1.n>0时根结点是唯一的，不可能存在多个根结点,应与现实中的大树区分开
 　　2.m>0时，子树的个数没有限制，但它们一定是互不相交的。

结点分类：

　　结点拥有的子树称为结点的度(Degree).

　　度为0的结点称为叶结点(Leaf)或终端结点；

　　度不为0的结点称为非终端结点或分支结点。

　　除根结点外，分支节点也称为内部结点。

　　树的度是树内各结点的度的最大值

结点间关系：
　　结点的子树的根称为该节点的孩子(Child),相应地，该结点称为孩子的双亲(Parent).
　　同一个双亲的孩子之间的互称兄弟(Sibling).
　　结点的祖先是从根到该节点所经分支上的所有节点。
　　以某结点为根的子树中的任一结点都称为该结点的子孙。

树的其他相关概念：
　　结点的层次(Level)从根开始定义起，根为第一层，根的孩子为第二层。
　　双亲在同一层的结点互为堂兄弟。
　　树中结点的最大层次称为树的深度(Depth)或高度。

 　　如果将树中结点的各子树看成从左至右是有次序的，不能互换的，则称该数为有序树，否则称为无序树。
　　 森林(Forest)是m(m>=0)棵互不相交的树的集合。

对比线性表与树的结构：
 线性结构：
  　　第一个数据元素：无前驱
 　　 最后一个数据元素：无后继
  　　中间元素：一个前驱一个后继
 树结构：
  　　根结点：无双亲，唯一
  　　叶结点：无孩子，可以多个
  　　中间结点：一个双亲多个孩子（或一个孩子）

树的抽象数据类型：

    ADT 树(Tree)
    Data
        树是由一个根结点和若干棵子树构成。树中结点具有相同数据类型及层次关系。
    Operation
        InitTree(*T):构造空树T.
        DestroyTree(*T):销毁树T.
        CreateTree(*T,definition):按difinition中给出树的定义来构造树。
        ClearTree(*T):若树T存在，则将树T清为空树。
        TreeEmpty(T):若T为空树，返回true，否则返回false.
        TreeDepth(T):返回T的深度。
        Root(T):返回T的根结点。
        Value(T,cur_e):cur_e是树T中的一个结点，返回此结点的值。
        Assign(T,cur_e,value):给树T的结点cur_e赋值为value.
        Parent(T,cur_e):若cur_e是树的非根结点，则返回它的双亲，否则返回空。
        LeftChild(T,cur_e):若cur_e是树的非叶结点，则返回它的最左孩子，否则返回空。
        RightSibling(T,cur_e):若cur_e有右兄弟，则返回它的右兄弟，否则返回空。
        InsertChild(*T,*p,i,c):其中p指向树的某个结点，i为所指结点p的度加上1，非空树c与T不相交，操作结果为插入c为树T中p指结点的第i棵子树。
        DeleteChild(*T,*p,i):其中p指向树T的某个结点，i为所指结点的p的度，操作结果为删除T中p所指结点的第i棵子树。
    endADT

树的存储结构：
　　　　双亲表示法：我们假设以一组连续空间存储树的结点，同时在每个结点中，附设一个指示器指示其双亲结点在数组中的位置。

　　　　　　　　　　---即每个结点除了知道自己是谁之外，还知道它的双亲在哪。

 其结点结构如下所示：
 

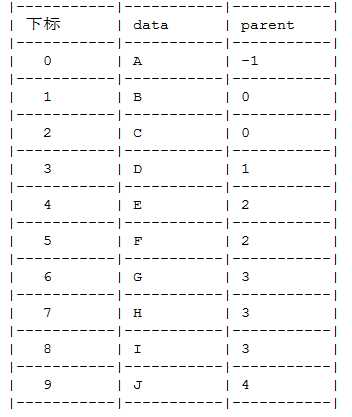
　　其中data为数据域，存储结点的数据信息，parent是指针域，存储该结点的双亲在数组中的下标。

　　以下为双亲表示法的结点结构定义代码：

    #define MAX_TREE_SIZE 100
    typedef int TElemType;
    typedef struct PTNode
    {
        TElemType data;
        int parent;
    }PTNode;
    typedef struct
    {
        PTNode nodes[MAX_TREE_SIZE];
        int r,n;//根的位置和结点数
    }PTree;

　　以下是一颗树的表示：

　　此外还可以有以下类型的表示法（只是一部分）：

　　存储结构的设计是一个非常灵活的过程，一个存储结构设计得是否合理，取决于基于该存储结构的运算是否合适、是否方便，时间复杂度好不好等。

孩子表示法：

　　　　多重链表表示法：每个结点由多个指针域，其中每个指针指向一棵子树的根结点，我们把这种方法叫做多重链表表示法。
　　　　以下有两种方案解决孩子个数不同的问题。

 　　其中data为数据域，child1到childn为指针域，用来指向该结点的孩子结点。
 　　优缺点分析：这种方法对于树中各结点的度相差很大时，显然是浪费空间的，因为有很多的结点，其指针域都是空的，

　　　　　　　　但是如果各个结点的度相差不大时，就意味着空间被充分的利用了，这时存储结构的缺点反而变成了优点。
 
 　　　鉴于上述第一种方案可能带来空间上的浪费的问题，我们提出了方案二：
　方案二：
  　　第二种方案每个结点指针域的个数等于该结点的度，我们专门取一个位置来存储结点指针域的个数，其结构如下：

　　其中data为数据域，degree为度域，也就是存储该结点的孩子结点的个数，child1到childn为指针域，指向该结点的各个孩子的结点。
　　优缺点分析：这种方案客服了浪费空间的缺点，对空间的利用率是很高了，但是由于各个结点的链表是不相同的结构，

　　　　　　　　加上要维护结点的度的数值，在运算上就会带来时间上的损耗。
 
　　鉴于上述的多重链表表示法的两种方案都不是很适合，所以我们引入孩子表示法这个概念：

　　　　具体的办法就是，把每个结点的孩子结点排列起来，以单链表作存储结构，则n个结点有n个孩子链表，

　　　　如果是叶子结点则此单链表为空。然后n个头指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中，具体的表示如下所示：

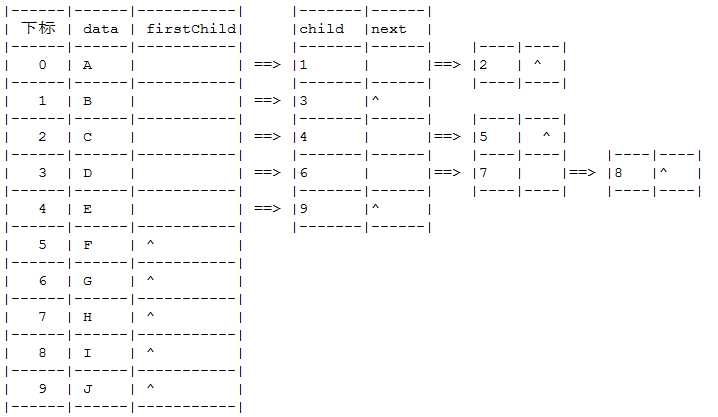
　　为此需要设计两种结点结构，一个是孩子链表的孩子结点

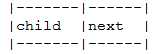
 　　其中child是数据域，用来存储某个结点在表头数组中的下标，next是指针域，用来存储指向某结点的下一个孩子结点的指针。
 　　另一个是表头数组的表头结点

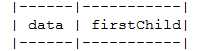
　　其中data为数据域，存储某结点的数据信息，firstchild是头指针域，存储该结点的孩子链表的头指针。
 
 以下为孩子表示法的结构定义代码：

    #define MAX_TREE_SIZE 100
    typedef struct CTNode
    {
        int child;
        struct CTNode *next;
    }*ChildPtr;
    typedef struct
    {
        TElemType data;
        ChildPtr firstchild;
    }CTBox;
    typedef struct
    {
        CTBox nodes[MAX_TREE_SIZE];
        int r,n;//根的位置和结点数
    }CTree;

　　以上的结构对于我们要查找某个结点的某个孩子，或者找某个结点的兄弟，只需要查找这个结点的孩子单链表即可，对于遍历整棵树也是很方便的，对头结点的数组循环即可。
 
　　如果需要查找某个结点的双亲结点是谁的话，则可以考虑一下这种结构

　　以上的表示法称为双亲孩子表示法

　　孩子兄弟表示法：  任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的。

　　　　　　　　　　　因此，我们设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟。

 　　其中data为数据域，firstchild为指针域，存储该结点的第一个孩子结点的存储地址，rightsib是指针域，存储该结点的右兄弟结点的存储地址。

结构定义代码如下。

    typedef struct CSNode
    {
        TElemType data;
        struct CSNode *firstchild,*rightsib;
    }CSNode,*CSTree;

　　　分析：这种表示法，给查找某个结点的某个孩子带来了方便，只需要通过firstchild找到此结点的长子，然后再通过长子结点的rightsib找到它的二弟，接着一直下去，知道找到具体的孩子。当然，如果想找某个结点的双亲，这个表示法也是有缺陷的。当然也可以增加一个双亲指针域来解决快速查找双亲的问题，这样其实表示出来的图示就是一个二叉树。二叉树的内容，放到下一复习小节。

数据结构看书笔记（六）--树

原文：http://www.cnblogs.com/lazyfennec/p/6289141.html