本系列意在长期连载分享，内容上可能也会有所增删改减；
因此如果转载，请务必保留源地址，非常感谢！
知乎专栏：https://zhuanlan.zhihu.com/data-miner
博客园：http://www.cnblogs.com/data-miner（暂时公式显示有问题）

当我们在谈论kmeans：其他聚类算法

Fuzzy C-Means (FCM)

　　Fuzzy C-Means 是一种模糊聚类算法。K-means中每一个元素只能属于一个类别，而Fuzzy C-Means中一个元素以不同的概率属于每一个类别。

　　Fuzzy C-Means最早出自J. C. Dunn. "A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters." 1973，而后在Bezdek, James C. Pattern recognition with fuzzy objective function algorithms, 1981书中被改进。由于后者是一本书，我就没有去翻看原著了。以下给出的是现在常用的版本

1. 类似于K-means，FCM的损失函数如下
   
   其中，满足如下限制
   

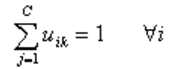
2. 求取FCM损失函数极小值，依然是迭代进行，步骤如下。其中参数更新的公式，可以通过对1中公式用拉格朗日法求解。

Hierarchical Clustering

　　Hierarchical Clustering即层次聚类。它有两种类型：

1. 自下而上：即最初将每个样本点看做一个类别，然后将最相似的两个样本聚合，迭代这个步骤，直到只有一个类别

2. 自上而下：即最初将所有样本看做一个类别，然后依据一定规则进行分裂，直到每个样本单独一个类别；这个方法在实际中应用很少

   　　Hierarchical Clustering最早出自Johnson, Stephen C. "Hierarchical clustering schemes." 1967，步骤如下：

3. Start by assigning each item to a cluster, so that if you have N items, you now have N clusters, each containing just one item. Let the distances (similarities) between the clusters the same as the distances (similarities) between the items they contain.
4. Find the closest (most similar) pair of clusters and merge them into a single cluster, so that now you have one cluster less.
5. Compute distances (similarities) between the new cluster and each of the old clusters.
6. Repeat steps 2 and 3 until all items are clustered into a single cluster of size N.

其中在步骤3中计算距离，有几种不同的计算方式：

1. single-linkage: 当计算两个cluster之间的距离时，计算这两个cluster中距离最短的两个点的距离
2. complete-linkage: 当计算两个cluster之间的距离时，计算这两个cluster中距离最长的两个点的距离
3. average-linkage: 当计算两个cluster之间的距离时，计算这两个cluster中两两样本点距离的均值
4. median-linkage: 当计算两个cluster之间的距离时，计算这两个cluster中两两样本点距离的中值

DBSCAN

　　DBSCAN即Density-Based Spatial Clustering of Applications with Noise，是一种基于密度的聚类算法，最早出自Ester, Martin, et al. "A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise." 1996。作者认为聚类算法应该尽量满足以下三点要求：

1. 需要的参数尽量的少。因为在实际分析场景中，一般对数据的先验信息所知甚少
2. 能有效针对不同形状的数据集。如K-means只能适用于凸的数据集

3. 对大规模数据的性能要好

   　　针对以上三点，作者提出了DBSCAN算法。这种算法本质是认为同一个类别的数据点集在空间中的密度是比较大的，而不同类别的数据集间的点在空间中密度很小。如下图，应该被分割成四个类别
   

   　　DBSCAN算法首先需要定义一些概念：

4. Ε邻域：设定半径为E，则以某对象为中心，半径为Ε内的区域称为该对象的Ε邻域
5. 核心对象：如果给定对象的Ε领域内的样本点数大于等于MinPts，则称该对象为核心对象
6. 直接密度可达：对于样本p、q，如果样本点q在p的Ε领域内，并且p为核心对象，那么称对象q从对象p直接密度可达
7. 密度可达：给定一系列样本点p1,p2….pn，p= p1,q= pn,假如对象pi从pi-1直接密度可达，那么对象q从对象p密度可达。

8. 密度相连：存在样本集合D中的一点o，如果对象o到对象p和对象q都是密度可达的，那么p和q密度相联

   　　DBSCAN算法的具体步骤如下（引用的DBSCAN伪代码，比原文中的易懂）

DBSCAN(D, eps, MinPts) {
    # 找到核心对象P
   C = 0
   for each point P in dataset D {
      if P is visited
         continue next point
      mark P as visited
      NeighborPts = regionQuery(P, eps)
      if sizeof(NeighborPts) < MinPts
         mark P as NOISE
      else {
         C = next cluster
         expandCluster(P, NeighborPts, C, eps, MinPts)
      }
   }
}
expandCluster(P, NeighborPts, C, eps, MinPts) {
    # 找到所有从核心对象P密度可达的点
   add P to cluster C
   for each point P‘‘ in NeighborPts {
      if P‘‘ is not visited {
         mark P‘‘ as visited
         NeighborPts‘‘ = regionQuery(P‘‘, eps)
         if sizeof(NeighborPts‘‘) >= MinPts
            NeighborPts = NeighborPts joined with NeighborPts‘‘
      }
      if P‘‘ is not yet member of any cluster
         add P‘‘ to cluster C
   }
}
regionQuery(P, eps)
# 查询点P的E邻域的点集
   return all points within P‘‘s eps-neighborhood (including P)

原文中还有如何探索式的选择合适的参数，这里不再赘述。

Mixture of Gaussians

Density Peaks

当我们在谈论kmeans（4）

原文：http://www.cnblogs.com/data-miner/p/6298468.html