——没有什么是一个BFS或一个DFS解决不了的;如果有,那就两个一起。
最大流的EK算法虽然简单,但时间复杂度是O(nm2),在竞赛中不太常用。
竞赛中常用的Dinic算法和SAP,其实也不太难。
那么,Dinic算法到底是什么呢?
多路增广
Dinic算法最核心的内容就是多路增广。
沿着EK算法的过程:
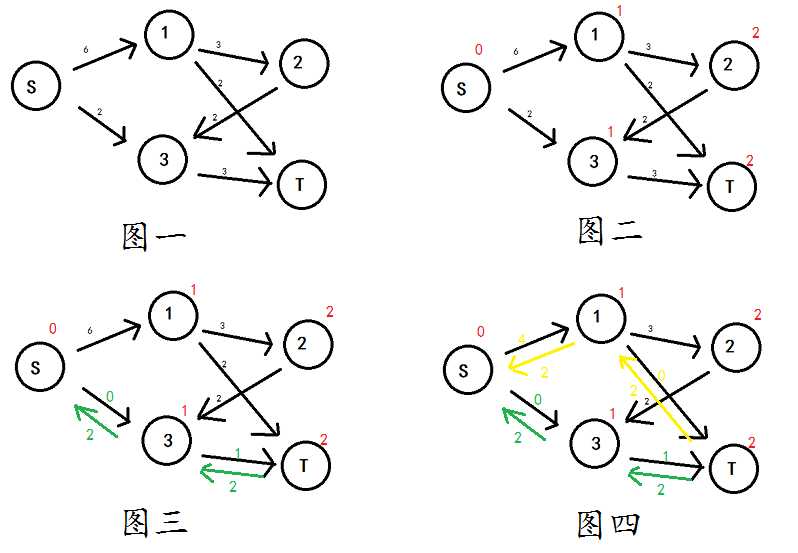
我们有一个图,如图一。
按照套路,我们先BFS,找S-T最短路。所有的距离标号都画在了图二上(EK算法可能用不到,但Dinic用得到)。
假设我们选的是S-3-T这条路,增广。。。(如图三,绿色)
然后我们再来一遍BFS。。。 等等!
细心的你可能也发现了,S-1-T也是一条S-T最短路。
那就增光吧!(如图四)
您可以检查一下,这时候没有长度为2的最短路了。
但EK算法不会这样。它会再笨拙地BFS一遍,这就浪费了不少时间。
所以说,多路增广是很重要的。
我们换一种思路,如果网络流在一个DAG上,还不用考虑回退边,你会怎么做?
这很简单,dfs就能解决。
至于回退边。。。再来一次BFS-DFS就好了啊。
附代码!
1 struct Dinic{ 2 struct Edge{ 3 int from, to; 4 LL cap, flow; 5 Edge(int f = -1, int t = -1, LL c = 0) 6 :from(f), to(t), cap(c) 7 {} 8 }edges[MAXM]; 9 int next[MAXM], cnt; 10 int pre[MAXN], dis[MAXN]; 11 Dinic() 12 { 13 memset(pre, -1, sizeof(pre)); 14 cnt = 0; 15 } 16 void addedge(int f, int t, LL c) 17 { 18 edges[cnt] = Edge(f, t, c); 19 next[cnt] = pre[f]; 20 pre[f] = cnt++; 21 edges[cnt] = Edge(t, f, 0); 22 next[cnt] = pre[t]; 23 pre[t] = cnt++; 24 } 25 queue<int> Q; 26 bool BFS(int s, int t) 27 { 28 while(!Q.empty()) Q.pop(); 29 memset(dis, -1, sizeof(dis)); 30 dis[s] = 0; 31 while(!Q.empty()) 32 { 33 int u = Q.front(); Q.pop(); 34 for(int i = pre[u]; i >= 0; i = next[i]) if(edges[i].cap > edges[i].flow) 35 { 36 int v = edges[i].to; 37 if(dis[v] >= 0) continue; 38 dis[v] = dis[u] + 1; 39 if(v == t) return true; 40 Q.push(v); 41 } 42 } 43 return false; 44 } 45 LL DFS(int now, int t, LL maxflow) //当前在now,汇点t 46 { // 最大可以提供maxflow的流量 47 if(now == t) return maxflow; 48 int ret = 0; 49 for(int i = pre[now]; i >= 0; i = next[i]) if(edges[i].cap > edges[i].flow) 50 { 51 int v = edges[i].to; 52 if(dis[v] != dis[now] + 1) continue; 53 int l = DFS(v, t, min(edges[i].cap - edges[i].flow, maxflow - ret)); 54 ret += l; 55 edges[i].flow += l; 56 edges[i^1].flow -= l; 57 if(ret == maxflow) return ret; 58 } 59 return ret; 60 } 61 LL solve(int s, int t) 62 { 63 int res = 0; 64 while(BFS(s,t)) res += DFS(s, t, inf); 65 return res; 66 } 67 }; 68
代码可能有错,烦请指出。谢谢。
另外,如果有人知道些好用的画图软件麻烦推荐一下。用windows自带画图太累了。
原文:http://www.cnblogs.com/y-clever/p/6308820.html